Question Number 155497 by VIDDD last updated on 01/Oct/21

Answered by amin96 last updated on 01/Oct/21
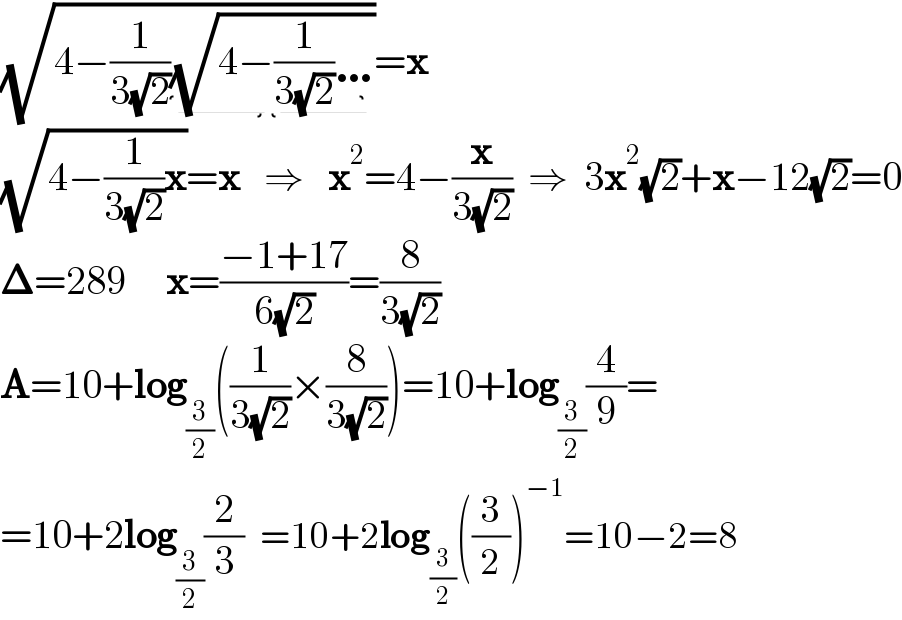
$$\sqrt{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\underbrace{\sqrt{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\ldots}}}=\boldsymbol{\mathrm{x}}\:\: \\ $$$$\sqrt{\mathrm{4}−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\boldsymbol{\mathrm{x}}}=\boldsymbol{\mathrm{x}}\:\:\:\Rightarrow\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\mathrm{4}−\frac{\boldsymbol{\mathrm{x}}}{\mathrm{3}\sqrt{\mathrm{2}}}\:\:\Rightarrow\:\:\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \sqrt{\mathrm{2}}+\boldsymbol{\mathrm{x}}−\mathrm{12}\sqrt{\mathrm{2}}=\mathrm{0} \\ $$$$\boldsymbol{\Delta}=\mathrm{289}\:\:\:\:\:\boldsymbol{\mathrm{x}}=\frac{−\mathrm{1}+\mathrm{17}}{\mathrm{6}\sqrt{\mathrm{2}}}=\frac{\mathrm{8}}{\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$$\boldsymbol{\mathrm{A}}=\mathrm{10}+\boldsymbol{\mathrm{log}}_{\frac{\mathrm{3}}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}×\frac{\mathrm{8}}{\mathrm{3}\sqrt{\mathrm{2}}}\right)=\mathrm{10}+\boldsymbol{\mathrm{log}}_{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\mathrm{4}}{\mathrm{9}}= \\ $$$$=\mathrm{10}+\mathrm{2}\boldsymbol{\mathrm{log}}_{\frac{\mathrm{3}}{\mathrm{2}}} \frac{\mathrm{2}}{\mathrm{3}}\:\:=\mathrm{10}+\mathrm{2}\boldsymbol{\mathrm{log}}_{\frac{\mathrm{3}}{\mathrm{2}}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{−\mathrm{1}} =\mathrm{10}−\mathrm{2}=\mathrm{8} \\ $$
Commented by puissant last updated on 01/Oct/21
$${Nice}\:{Sir}\:{really}\:{great}… \\ $$
Commented by VIDDD last updated on 01/Oct/21

$${great}\:{sir}\:,{thanks} \\ $$
