Question-155500

Question Number 155500 by VIDDD last updated on 01/Oct/21

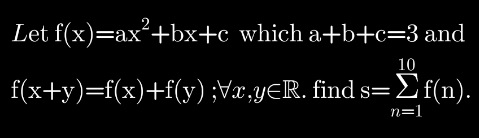
Answered by MJS_new last updated on 01/Oct/21

f(x+y)−(f(x)+f(y))=0 2axy−c=0 this is only true ∀x,y∈R with a=0 ⇒ c=0 a+b+c=3 ⇒ b=3 f(x)=3x the rest is easy

$${f}\left({x}+{y}\right)−\left({f}\left({x}\right)+{f}\left({y}\right)\right)=\mathrm{0} \\ $$$$\mathrm{2}{axy}−{c}=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{only}\:\mathrm{true}\:\forall{x},{y}\in\mathbb{R}\:\mathrm{with}\:{a}=\mathrm{0}\:\Rightarrow\:{c}=\mathrm{0} \\ $$$${a}+{b}+{c}=\mathrm{3}\:\Rightarrow\:{b}=\mathrm{3} \\ $$$${f}\left({x}\right)=\mathrm{3}{x} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$

Commented by VIDDD last updated on 01/Oct/21

$${greay}\:{sir}\:;\:{thanks} \\ $$

Commented by puissant last updated on 01/Oct/21

f(n)=3n ⇒ Σ_(n=1) ^(10) f(n)=Σ_(n=1) ^(10) 3n=3Σ_(n=1) ^(10) n=3•((10×11)/2) =3×55= 165...

$${f}\left({n}\right)=\mathrm{3}{n} \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{f}\left({n}\right)=\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\mathrm{3}{n}=\mathrm{3}\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{n}=\mathrm{3}\bullet\frac{\mathrm{10}×\mathrm{11}}{\mathrm{2}} \\ $$$$=\mathrm{3}×\mathrm{55}=\:\mathrm{165}… \\ $$

Answered by Rasheed.Sindhi last updated on 02/Oct/21

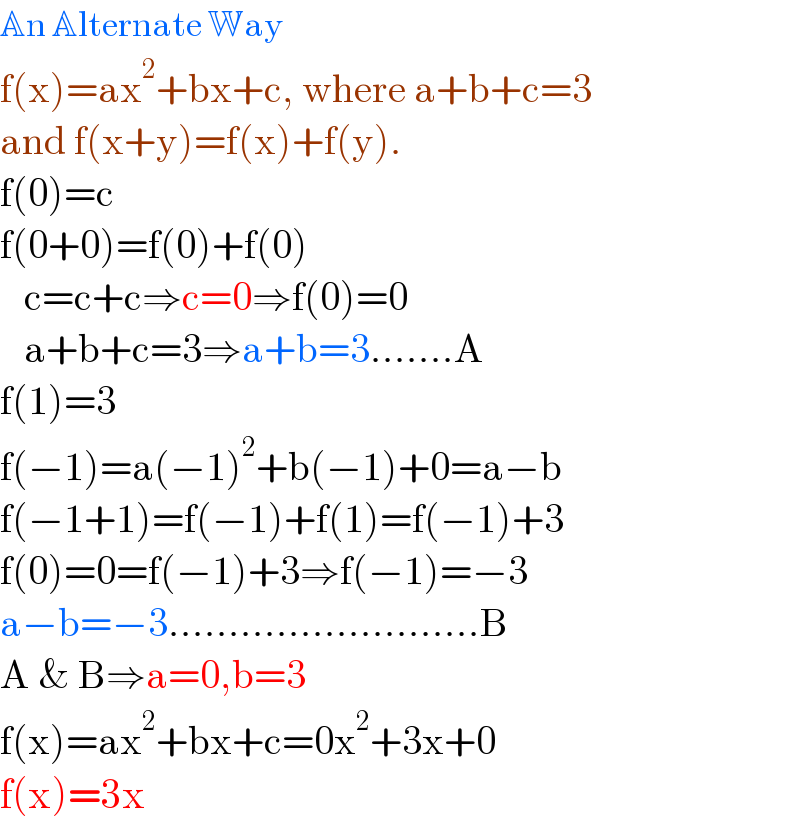
An Alternate Way f(x)=ax^2 +bx+c, where a+b+c=3 and f(x+y)=f(x)+f(y). f(0)=c f(0+0)=f(0)+f(0) c=c+c⇒c=0⇒f(0)=0 a+b+c=3⇒a+b=3.......A f(1)=3 f(−1)=a(−1)^2 +b(−1)+0=a−b f(−1+1)=f(−1)+f(1)=f(−1)+3 f(0)=0=f(−1)+3⇒f(−1)=−3 a−b=−3..........................B A & B⇒a=0,b=3 f(x)=ax^2 +bx+c=0x^2 +3x+0 f(x)=3x

$$\mathbb{A}\mathrm{n}\:\mathbb{A}\mathrm{lternate}\:\mathbb{W}\mathrm{ay} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c},\:\mathrm{where}\:\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{3} \\ $$$$\mathrm{and}\:\mathrm{f}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{y}\right). \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{0}+\mathrm{0}\right)=\mathrm{f}\left(\mathrm{0}\right)+\mathrm{f}\left(\mathrm{0}\right) \\ $$$$\:\:\:\mathrm{c}=\mathrm{c}+\mathrm{c}\Rightarrow\mathrm{c}=\mathrm{0}\Rightarrow\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\:\:\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{3}\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{3}…….\mathrm{A} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{3} \\ $$$$\mathrm{f}\left(−\mathrm{1}\right)=\mathrm{a}\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{b}\left(−\mathrm{1}\right)+\mathrm{0}=\mathrm{a}−\mathrm{b} \\ $$$$\mathrm{f}\left(−\mathrm{1}+\mathrm{1}\right)=\mathrm{f}\left(−\mathrm{1}\right)+\mathrm{f}\left(\mathrm{1}\right)=\mathrm{f}\left(−\mathrm{1}\right)+\mathrm{3} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}=\mathrm{f}\left(−\mathrm{1}\right)+\mathrm{3}\Rightarrow\mathrm{f}\left(−\mathrm{1}\right)=−\mathrm{3} \\ $$$$\mathrm{a}−\mathrm{b}=−\mathrm{3}……………………..\mathrm{B} \\ $$$$\mathrm{A}\:\&\:\mathrm{B}\Rightarrow\mathrm{a}=\mathrm{0},\mathrm{b}=\mathrm{3} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}=\mathrm{0x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3x} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply