Question Number 155506 by VIDDD last updated on 01/Oct/21
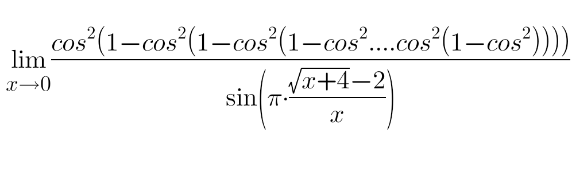
Answered by amin96 last updated on 01/Oct/21
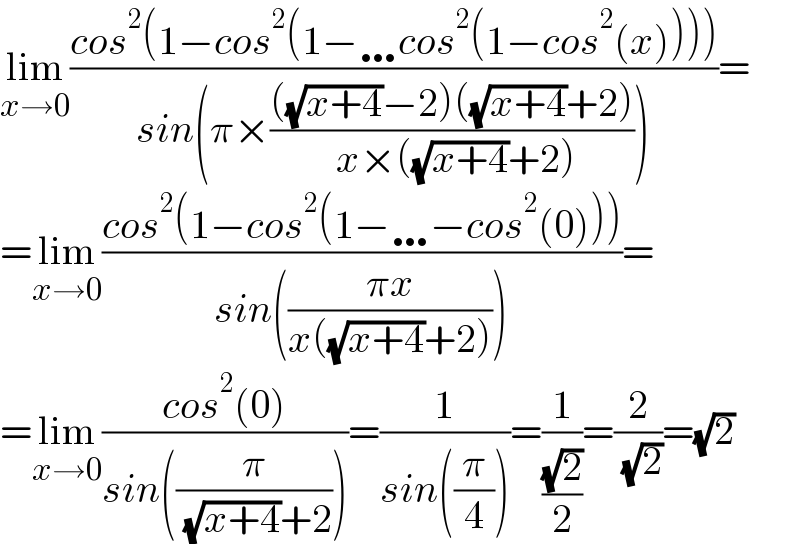
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{cos}^{\mathrm{2}} \left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\mathrm{1}−\ldots{cos}^{\mathrm{2}} \left(\mathrm{1}−{cos}^{\mathrm{2}} \left({x}\right)\right)\right)\right)}{{sin}\left(\pi×\frac{\left(\sqrt{{x}+\mathrm{4}}−\mathrm{2}\right)\left(\sqrt{{x}+\mathrm{4}}+\mathrm{2}\right)}{\:{x}×\left(\sqrt{{x}+\mathrm{4}}+\mathrm{2}\right)}\right)}= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{cos}^{\mathrm{2}} \left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\mathrm{1}−\ldots−{cos}^{\mathrm{2}} \left(\mathrm{0}\right)\right)\right)}{{sin}\left(\frac{\pi{x}}{{x}\left(\sqrt{{x}+\mathrm{4}}+\mathrm{2}\right)}\right)}= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{cos}^{\mathrm{2}} \left(\mathrm{0}\right)}{{sin}\left(\frac{\pi}{\:\sqrt{{x}+\mathrm{4}}+\mathrm{2}}\right)}=\frac{\mathrm{1}}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}=\sqrt{\mathrm{2}} \\ $$
