Question-155561

Question Number 155561 by peter frank last updated on 02/Oct/21

Answered by mr W last updated on 02/Oct/21

p_1 =pressure inside bubble at radius r p_2 =pressure inside bubble at radius 2r p_1 −p_0 =((4γ)/r) ⇒p_1 =p_0 +((4γ)/r) p_2 −p=((4γ)/(2r)) ⇒p_2 =p+((2γ)/r) (p_2 /p_1 )=(V_1 /V_2 )=((r/(2r)))^3 =(1/8) p+((2γ)/r)=(1/8)(p_0 +((4γ)/r)) p=(1/8)(p_0 +((4γ)/r))−((2γ)/r) ⇒p=(1/8)(p_0 −((12γ)/r))

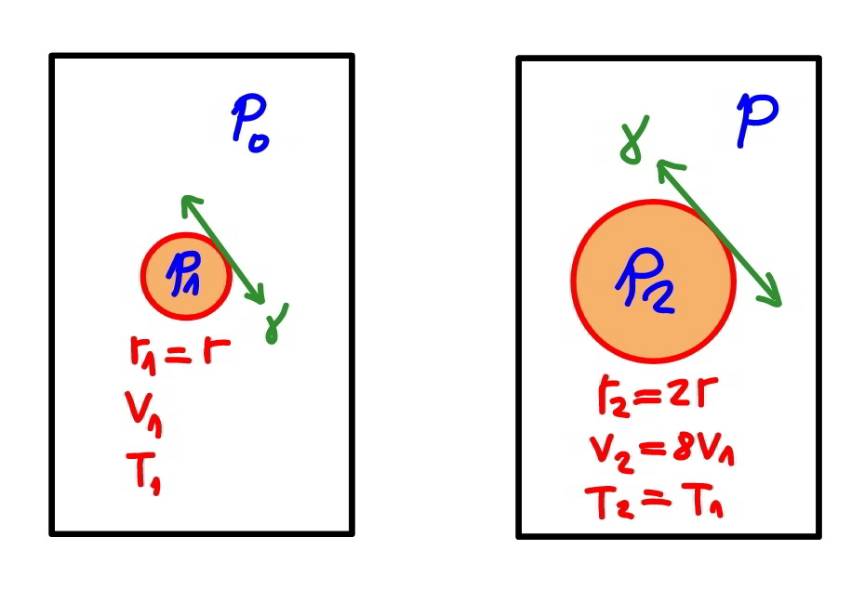
$${p}_{\mathrm{1}} ={pressure}\:{inside}\:{bubble}\:{at}\:{radius}\:{r} \\ $$$${p}_{\mathrm{2}} ={pressure}\:{inside}\:{bubble}\:{at}\:{radius}\:\mathrm{2}{r} \\ $$$${p}_{\mathrm{1}} −{p}_{\mathrm{0}} =\frac{\mathrm{4}\gamma}{{r}}\:\Rightarrow{p}_{\mathrm{1}} ={p}_{\mathrm{0}} +\frac{\mathrm{4}\gamma}{{r}} \\ $$$${p}_{\mathrm{2}} −{p}=\frac{\mathrm{4}\gamma}{\mathrm{2}{r}}\:\Rightarrow{p}_{\mathrm{2}} ={p}+\frac{\mathrm{2}\gamma}{{r}} \\ $$$$\frac{{p}_{\mathrm{2}} }{{p}_{\mathrm{1}} }=\frac{{V}_{\mathrm{1}} }{{V}_{\mathrm{2}} }=\left(\frac{{r}}{\mathrm{2}{r}}\right)^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${p}+\frac{\mathrm{2}\gamma}{{r}}=\frac{\mathrm{1}}{\mathrm{8}}\left({p}_{\mathrm{0}} +\frac{\mathrm{4}\gamma}{{r}}\right) \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{8}}\left({p}_{\mathrm{0}} +\frac{\mathrm{4}\gamma}{{r}}\right)−\frac{\mathrm{2}\gamma}{{r}} \\ $$$$\Rightarrow{p}=\frac{\mathrm{1}}{\mathrm{8}}\left({p}_{\mathrm{0}} −\frac{\mathrm{12}\gamma}{{r}}\right) \\ $$

Commented by mr W last updated on 02/Oct/21