Question Number 15558 by ajfour last updated on 11/Jun/17

Commented by ajfour last updated on 11/Jun/17
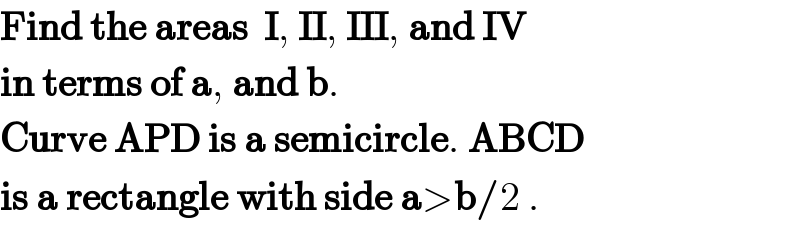
$$\boldsymbol{\mathrm{Find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{areas}}\:\:\boldsymbol{\mathrm{I}},\:\boldsymbol{\mathrm{II}},\:\boldsymbol{\mathrm{III}},\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{IV}} \\ $$$$\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{terms}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{a}},\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{b}}. \\ $$$$\boldsymbol{\mathrm{Curve}}\:\boldsymbol{\mathrm{APD}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{semicircle}}.\:\boldsymbol{\mathrm{ABCD}} \\ $$$$\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{rectangle}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{side}}\:\boldsymbol{\mathrm{a}}>\boldsymbol{\mathrm{b}}/\mathrm{2}\:. \\ $$
Answered by mrW1 last updated on 11/Jun/17
![α=tan^(−1) (a/b) ∠DOP=π−2α A_(III) =(1/2)((b/2))^2 [π−2α−sin (π−2α)] =(b^2 /8)[π−2α−sin 2α] =(b^2 /8)[π−2α−2×((ab)/(a^2 +b^2 ))] =(b^2 /4)[(π/2)−tan^(−1) (a/b)−((ab)/(a^2 +b^2 ))] A_(IV) =(π/2)((b/2))^2 −A_(III) =(b^2 /4)[tan^(−1) (a/b)+((ab)/(a^2 +b^2 ))] A_(II) =((ab)/2)−A_(III) =((ab)/2)−(b^2 /4)[(π/2)−tan^(−1) (a/b)−((ab)/(a^2 +b^2 ))] A_I =((ab)/2)−A_(IV) =((ab)/2)−(b^2 /4)[tan^(−1) (a/b)+((ab)/(a^2 +b^2 ))]](https://www.tinkutara.com/question/Q15563.png)
$$\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{a}}{\mathrm{b}} \\ $$$$\angle\mathrm{DOP}=\pi−\mathrm{2}\alpha \\ $$$$ \\ $$$$\mathrm{A}_{\mathrm{III}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)^{\mathrm{2}} \left[\pi−\mathrm{2}\alpha−\mathrm{sin}\:\left(\pi−\mathrm{2}\alpha\right)\right] \\ $$$$=\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{8}}\left[\pi−\mathrm{2}\alpha−\mathrm{sin}\:\mathrm{2}\alpha\right] \\ $$$$=\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{8}}\left[\pi−\mathrm{2}\alpha−\mathrm{2}×\frac{\mathrm{ab}}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\right] \\ $$$$=\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{4}}\left[\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{a}}{\mathrm{b}}−\frac{\mathrm{ab}}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\right] \\ $$$$ \\ $$$$\mathrm{A}_{\mathrm{IV}} =\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{A}_{\mathrm{III}} \\ $$$$=\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{4}}\left[\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{a}}{\mathrm{b}}+\frac{\mathrm{ab}}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\right] \\ $$$$ \\ $$$$\mathrm{A}_{\mathrm{II}} =\frac{\mathrm{ab}}{\mathrm{2}}−\mathrm{A}_{\mathrm{III}} \\ $$$$=\frac{\mathrm{ab}}{\mathrm{2}}−\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{4}}\left[\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{a}}{\mathrm{b}}−\frac{\mathrm{ab}}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\right] \\ $$$$ \\ $$$$\mathrm{A}_{\mathrm{I}} =\frac{\mathrm{ab}}{\mathrm{2}}−\mathrm{A}_{\mathrm{IV}} \\ $$$$=\frac{\mathrm{ab}}{\mathrm{2}}−\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{4}}\left[\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{a}}{\mathrm{b}}+\frac{\mathrm{ab}}{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\right] \\ $$
Commented by mrW1 last updated on 11/Jun/17

