Question-15561

Question Number 15561 by Mr easymsn last updated on 11/Jun/17

Commented by Mr easymsn last updated on 11/Jun/17

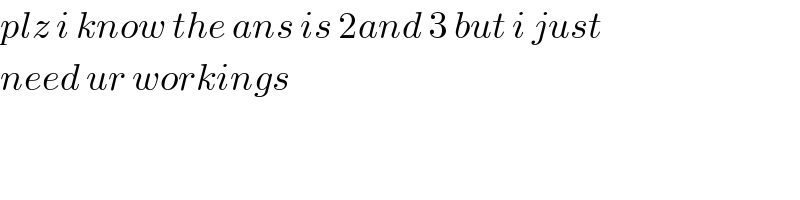
plz i know the ans is 2and 3 but i just need ur workings

$${plz}\:{i}\:{know}\:{the}\:{ans}\:{is}\:\mathrm{2}{and}\:\mathrm{3}\:{but}\:{i}\:{just} \\ $$$${need}\:{ur}\:{workings} \\ $$$$ \\ $$

Commented by RasheedSoomro last updated on 11/Jun/17

Both equations are symmetric that means if (a,b) satisfies the equations (b,a) also does In case x,y∈N possible values for x are 1,2,3,4 first equation suggests that respective values of y may be 4,3,2,1 So trying these values in second equation 1^4 +4^1 ≠17 2^3 +3^2 =8+9=17 Hence (2,3) & (3,2) are two solutions in N.

$$\mathrm{Both}\:\mathrm{equations}\:\mathrm{are}\:\mathrm{symmetric} \\ $$$$\mathrm{that}\:\mathrm{means}\:\mathrm{if}\:\left(\mathrm{a},\mathrm{b}\right)\:\mathrm{satisfies}\:\mathrm{the} \\ $$$$\mathrm{equations}\:\left(\mathrm{b},\mathrm{a}\right)\:\mathrm{also}\:\mathrm{does} \\ $$$$\mathrm{In}\:\mathrm{case}\:\mathrm{x},\mathrm{y}\in\mathbb{N} \\ $$$$\mathrm{possible}\:\mathrm{values}\:\mathrm{for}\:\mathrm{x}\:\mathrm{are}\:\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4} \\ $$$$\mathrm{first}\:\mathrm{equation}\:\mathrm{suggests}\:\mathrm{that}\:\mathrm{respective} \\ $$$$\mathrm{values}\:\mathrm{of}\:\mathrm{y}\:\mathrm{may}\:\mathrm{be}\:\mathrm{4},\mathrm{3},\mathrm{2},\mathrm{1} \\ $$$$\mathrm{So}\:\mathrm{trying}\:\mathrm{these}\:\mathrm{values}\:\mathrm{in}\:\mathrm{second}\:\mathrm{equation} \\ $$$$\mathrm{1}^{\mathrm{4}} +\mathrm{4}^{\mathrm{1}} \neq\mathrm{17} \\ $$$$\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{2}} =\mathrm{8}+\mathrm{9}=\mathrm{17} \\ $$$$\mathrm{Hence}\:\left(\mathrm{2},\mathrm{3}\right)\:\&\:\left(\mathrm{3},\mathrm{2}\right)\:\mathrm{are}\:\mathrm{two}\:\mathrm{solutions}\:\mathrm{in}\:\mathbb{N}. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

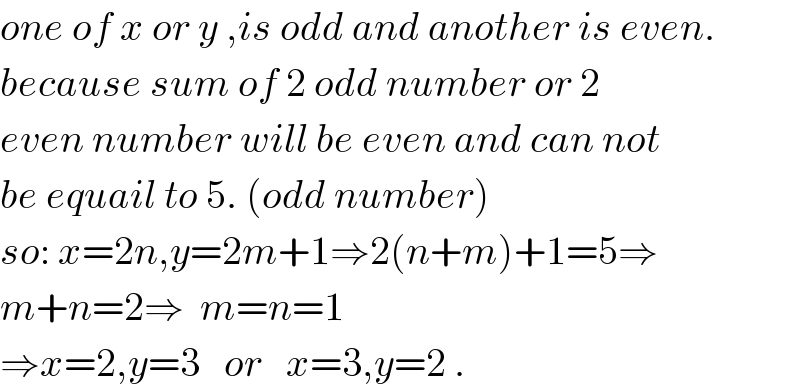
one of x or y ,is odd and another is even. because sum of 2 odd number or 2 even number will be even and can not be equail to 5. (odd number) so: x=2n,y=2m+1⇒2(n+m)+1=5⇒ m+n=2⇒ m=n=1 ⇒x=2,y=3 or x=3,y=2 .

$${one}\:{of}\:{x}\:{or}\:{y}\:,{is}\:{odd}\:{and}\:{another}\:{is}\:{even}. \\ $$$${because}\:{sum}\:{of}\:\mathrm{2}\:{odd}\:{number}\:{or}\:\mathrm{2}\: \\ $$$${even}\:{number}\:{will}\:{be}\:{even}\:{and}\:{can}\:{not} \\ $$$${be}\:{equail}\:{to}\:\mathrm{5}.\:\left({odd}\:{number}\right) \\ $$$${so}:\:{x}=\mathrm{2}{n},{y}=\mathrm{2}{m}+\mathrm{1}\Rightarrow\mathrm{2}\left({n}+{m}\right)+\mathrm{1}=\mathrm{5}\Rightarrow \\ $$$${m}+{n}=\mathrm{2}\Rightarrow\:\:{m}={n}=\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{2},{y}=\mathrm{3}\:\:\:{or}\:\:\:{x}=\mathrm{3},{y}=\mathrm{2}\:. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply