Question Number 155638 by cortano last updated on 03/Oct/21
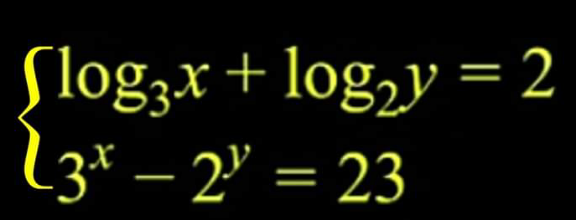
Commented by Rasheed.Sindhi last updated on 03/Oct/21

$${x}=\mathrm{3},{y}=\mathrm{2} \\ $$
Commented by cortano last updated on 03/Oct/21

$$\mathrm{by}\:?\: \\ $$
Answered by mindispower last updated on 03/Oct/21
![(x,y)∈R^2 ⇒x,y>0 if y∈]0,2[⇒log_3 (x)=2−log_2 (y)>1 ⇒x>3 3^x −2^y >3^3 −2^2 =23 y>2⇒log_3 (x)<2−log_2 (2)⇒x<3 3^x −2^y <3^3 −2^2 =23 y∈]0,2[∪]2,+∞[ no solution y=2⇒x=3 (3,2) is the solution](https://www.tinkutara.com/question/Q155717.png)
$$\left({x},{y}\right)\in\mathbb{R}^{\mathrm{2}} \Rightarrow{x},{y}>\mathrm{0} \\ $$$$\left.{if}\:{y}\in\right]\mathrm{0},\mathrm{2}\left[\Rightarrow{log}_{\mathrm{3}} \left({x}\right)=\mathrm{2}−{log}_{\mathrm{2}} \left({y}\right)>\mathrm{1}\right. \\ $$$$\Rightarrow{x}>\mathrm{3} \\ $$$$\mathrm{3}^{{x}} −\mathrm{2}^{{y}} >\mathrm{3}^{\mathrm{3}} −\mathrm{2}^{\mathrm{2}} =\mathrm{23} \\ $$$${y}>\mathrm{2}\Rightarrow{log}_{\mathrm{3}} \left({x}\right)<\mathrm{2}−{log}_{\mathrm{2}} \left(\mathrm{2}\right)\Rightarrow{x}<\mathrm{3} \\ $$$$\mathrm{3}^{{x}} −\mathrm{2}^{{y}} <\mathrm{3}^{\mathrm{3}} −\mathrm{2}^{\mathrm{2}} =\mathrm{23} \\ $$$$\left.{y}\in\right]\mathrm{0},\mathrm{2}\left[\cup\right]\mathrm{2},+\infty\left[\:{no}\:{solution}\right. \\ $$$${y}=\mathrm{2}\Rightarrow{x}=\mathrm{3} \\ $$$$\left(\mathrm{3},\mathrm{2}\right)\:{is}\:\:{the}\:{solution}\: \\ $$
