Question-155643

Question Number 155643 by zen17 last updated on 03/Oct/21

Commented by yeti123 last updated on 03/Oct/21

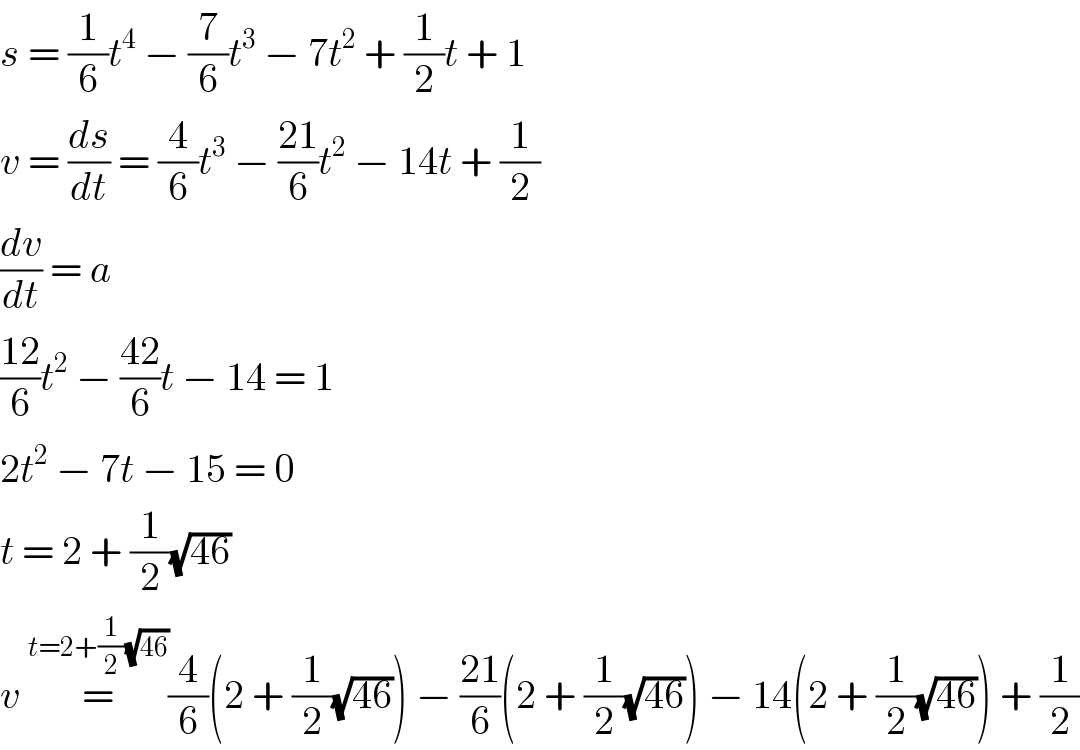
s = (1/6)t^4 − (7/6)t^3 − 7t^2 + (1/2)t + 1 v = (ds/dt) = (4/6)t^3 − ((21)/6)t^2 − 14t + (1/2) (dv/dt) = a ((12)/6)t^2 − ((42)/6)t − 14 = 1 2t^2 − 7t − 15 = 0 t = 2 + (1/2)(√(46)) v =^(t=2+(1/2)(√(46))) (4/6)(2 + (1/2)(√(46))) − ((21)/6)(2 + (1/2)(√(46))) − 14(2 + (1/2)(√(46))) + (1/2)

$${s}\:=\:\frac{\mathrm{1}}{\mathrm{6}}{t}^{\mathrm{4}} \:−\:\frac{\mathrm{7}}{\mathrm{6}}{t}^{\mathrm{3}} \:−\:\mathrm{7}{t}^{\mathrm{2}} \:+\:\frac{\mathrm{1}}{\mathrm{2}}{t}\:+\:\mathrm{1} \\ $$$${v}\:=\:\frac{{ds}}{{dt}}\:=\:\frac{\mathrm{4}}{\mathrm{6}}{t}^{\mathrm{3}} \:−\:\frac{\mathrm{21}}{\mathrm{6}}{t}^{\mathrm{2}} \:−\:\mathrm{14}{t}\:+\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{dv}}{{dt}}\:=\:{a} \\ $$$$\frac{\mathrm{12}}{\mathrm{6}}{t}^{\mathrm{2}} \:−\:\frac{\mathrm{42}}{\mathrm{6}}{t}\:−\:\mathrm{14}\:=\:\mathrm{1} \\ $$$$\mathrm{2}{t}^{\mathrm{2}} \:−\:\mathrm{7}{t}\:−\:\mathrm{15}\:=\:\mathrm{0} \\ $$$${t}\:=\:\mathrm{2}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{46}} \\ $$$${v}\:\overset{{t}=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{46}}} {=}\frac{\mathrm{4}}{\mathrm{6}}\left(\mathrm{2}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{46}}\right)\:−\:\frac{\mathrm{21}}{\mathrm{6}}\left(\mathrm{2}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{46}}\right)\:−\:\mathrm{14}\left(\mathrm{2}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{46}}\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Facebook Tweet Pin

Question-155643

Leave a Reply Cancel reply