Question Number 155701 by ajfour last updated on 03/Oct/21
Commented by ajfour last updated on 03/Oct/21
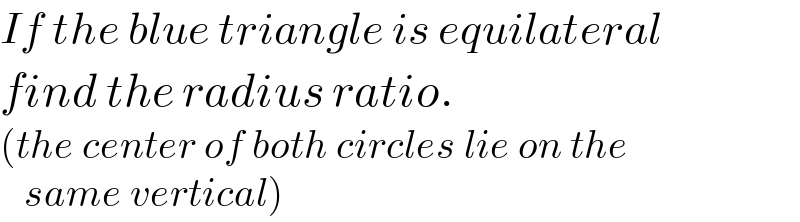
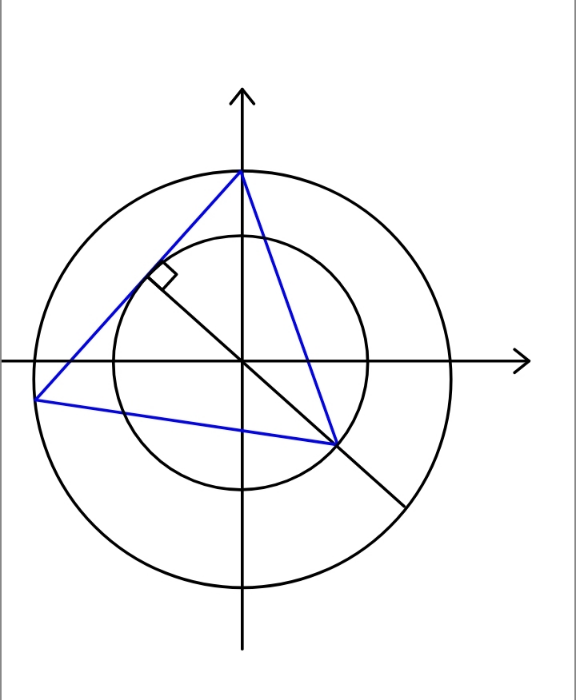
$${If}\:{the}\:{blue}\:{triangle}\:{is}\:{equilateral} \\ $$$${find}\:{the}\:{radius}\:{ratio}. \\ $$$$\left({the}\:{center}\:{of}\:{both}\:{circles}\:{lie}\:{on}\:{the}\right. \\ $$$$\left.\:\:\:{same}\:{vertical}\right) \\ $$
Commented by mr W last updated on 03/Oct/21
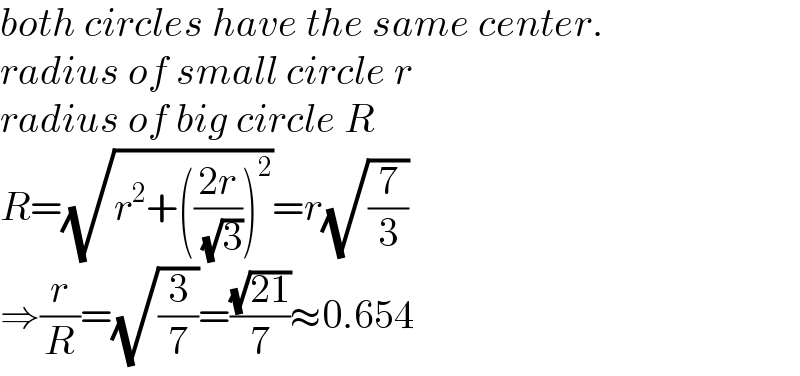
$${both}\:{circles}\:{have}\:{the}\:{same}\:{center}. \\ $$$${radius}\:{of}\:{small}\:{circle}\:{r} \\ $$$${radius}\:{of}\:{big}\:{circle}\:{R} \\ $$$${R}=\sqrt{{r}^{\mathrm{2}} +\left(\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }={r}\sqrt{\frac{\mathrm{7}}{\mathrm{3}}} \\ $$$$\Rightarrow\frac{{r}}{{R}}=\sqrt{\frac{\mathrm{3}}{\mathrm{7}}}=\frac{\sqrt{\mathrm{21}}}{\mathrm{7}}\approx\mathrm{0}.\mathrm{654} \\ $$
Commented by ajfour last updated on 04/Oct/21
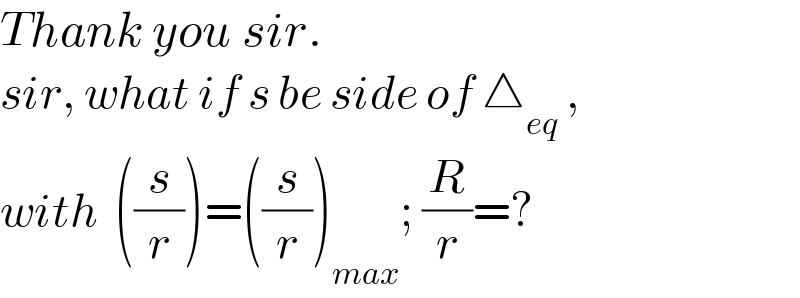
$${Thank}\:{you}\:{sir}. \\ $$$${sir},\:{what}\:{if}\:{s}\:{be}\:{side}\:{of}\:\bigtriangleup_{{eq}} \:, \\ $$$${with}\:\:\left(\frac{{s}}{{r}}\right)=\left(\frac{{s}}{{r}}\right)_{{max}} ;\:\frac{{R}}{{r}}=? \\ $$
