Question Number 155866 by cherokeesay last updated on 05/Oct/21

Answered by talminator2856791 last updated on 05/Oct/21
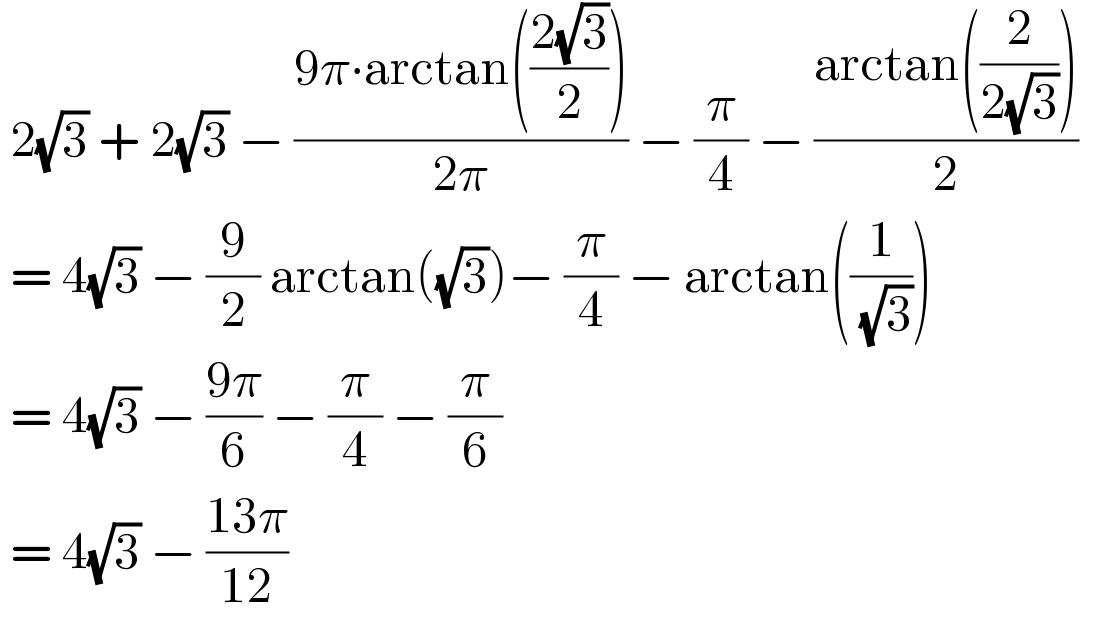
$$\:\mathrm{2}\sqrt{\mathrm{3}}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\:−\:\frac{\mathrm{9}\pi\centerdot\mathrm{arctan}\left(\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}{\mathrm{2}\pi}\:−\:\frac{\pi}{\mathrm{4}}\:−\:\frac{\mathrm{arctan}\left(\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3}}}\right)}{\mathrm{2}}\:\: \\ $$$$\:=\:\mathrm{4}\sqrt{\mathrm{3}}\:−\:\frac{\mathrm{9}}{\mathrm{2}}\:\mathrm{arctan}\left(\sqrt{\mathrm{3}}\right)−\:\frac{\pi}{\mathrm{4}}\:−\:\mathrm{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\:=\:\mathrm{4}\sqrt{\mathrm{3}}\:−\:\frac{\mathrm{9}\pi}{\mathrm{6}}\:−\:\frac{\pi}{\mathrm{4}}\:−\:\frac{\pi}{\mathrm{6}} \\ $$$$\:=\:\mathrm{4}\sqrt{\mathrm{3}}\:−\:\frac{\mathrm{13}\pi}{\mathrm{12}} \\ $$
Commented by cherokeesay last updated on 05/Oct/21

$$\frac{\mathrm{13}\pi}{\mathrm{12}}\:\left({error}\right) \\ $$
Commented by cherokeesay last updated on 05/Oct/21

$$\mathrm{4}\sqrt{\mathrm{3}}\:−\:\frac{\mathrm{11}\pi}{\mathrm{6}} \\ $$
