Question Number 156061 by mathlove last updated on 07/Oct/21

Answered by TheSupreme last updated on 07/Oct/21
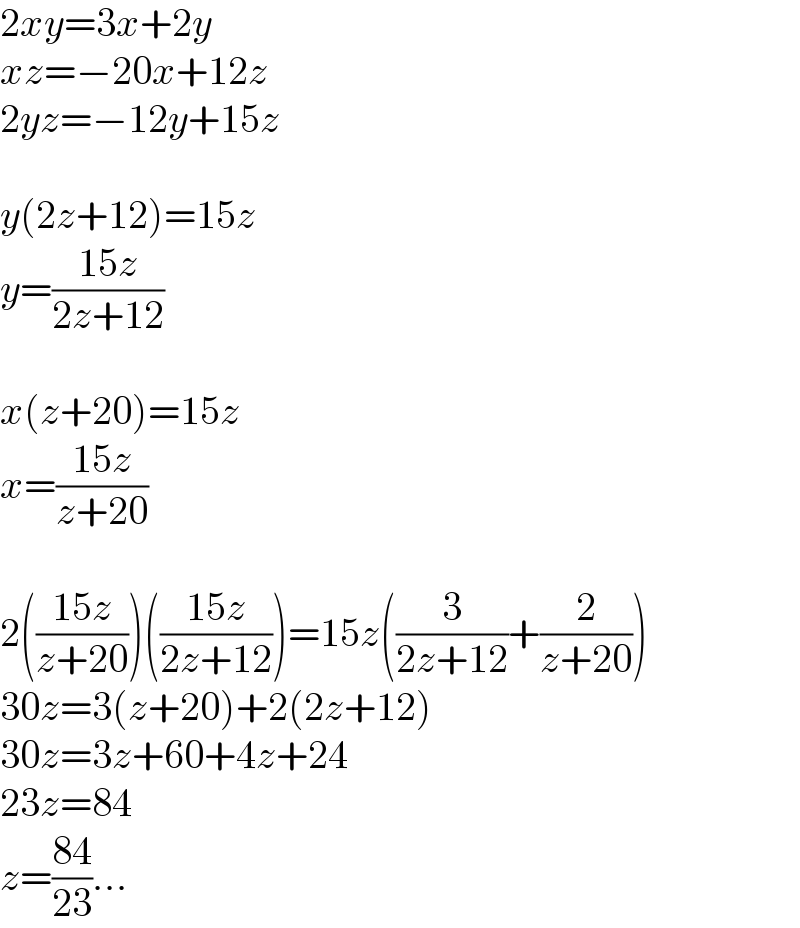
$$\mathrm{2}{xy}=\mathrm{3}{x}+\mathrm{2}{y} \\ $$$${xz}=−\mathrm{20}{x}+\mathrm{12}{z} \\ $$$$\mathrm{2}{yz}=−\mathrm{12}{y}+\mathrm{15}{z} \\ $$$$ \\ $$$${y}\left(\mathrm{2}{z}+\mathrm{12}\right)=\mathrm{15}{z} \\ $$$${y}=\frac{\mathrm{15}{z}}{\mathrm{2}{z}+\mathrm{12}} \\ $$$$ \\ $$$${x}\left({z}+\mathrm{20}\right)=\mathrm{15}{z} \\ $$$${x}=\frac{\mathrm{15}{z}}{{z}+\mathrm{20}} \\ $$$$ \\ $$$$\mathrm{2}\left(\frac{\mathrm{15}{z}}{{z}+\mathrm{20}}\right)\left(\frac{\mathrm{15}{z}}{\mathrm{2}{z}+\mathrm{12}}\right)=\mathrm{15}{z}\left(\frac{\mathrm{3}}{\mathrm{2}{z}+\mathrm{12}}+\frac{\mathrm{2}}{{z}+\mathrm{20}}\right) \\ $$$$\mathrm{30}{z}=\mathrm{3}\left({z}+\mathrm{20}\right)+\mathrm{2}\left(\mathrm{2}{z}+\mathrm{12}\right) \\ $$$$\mathrm{30}{z}=\mathrm{3}{z}+\mathrm{60}+\mathrm{4}{z}+\mathrm{24} \\ $$$$\mathrm{23}{z}=\mathrm{84} \\ $$$${z}=\frac{\mathrm{84}}{\mathrm{23}}… \\ $$
Answered by cortano last updated on 07/Oct/21

$$\:\begin{cases}{\frac{\mathrm{3x}+\mathrm{2y}}{\mathrm{xy}}=\mathrm{2}\Rightarrow\frac{\mathrm{3}}{\mathrm{y}}+\frac{\mathrm{2}}{\mathrm{x}}=\mathrm{2}}\\{\frac{\mathrm{5x}−\mathrm{3z}}{\mathrm{xz}}=−\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\frac{\mathrm{5}}{\mathrm{z}}−\frac{\mathrm{3}}{\mathrm{x}}=−\frac{\mathrm{1}}{\mathrm{4}}}\\{\frac{\mathrm{4y}−\mathrm{5z}}{\mathrm{yz}}=−\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow\frac{\mathrm{4}}{\mathrm{z}}−\frac{\mathrm{5}}{\mathrm{y}}=−\frac{\mathrm{2}}{\mathrm{3}}}\end{cases} \\ $$$$\begin{cases}{\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{a},\:\frac{\mathrm{1}}{\mathrm{y}}=\mathrm{b}\:,\frac{\mathrm{1}}{\mathrm{z}}=\mathrm{c}}\\{\mathrm{2a}+\mathrm{3b}=\mathrm{2}\:;\:−\mathrm{3a}+\mathrm{5c}=−\frac{\mathrm{1}}{\mathrm{4}}\:;\:−\mathrm{5b}+\mathrm{4c}=−\frac{\mathrm{2}}{\mathrm{3}}}\end{cases} \\ $$$$\Rightarrow\begin{pmatrix}{\mathrm{a}}\\{\mathrm{b}}\\{\mathrm{c}}\end{pmatrix}\:=\begin{pmatrix}{\:\:\:\:\mathrm{2}\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{0}}\\{−\mathrm{3}\:\:\:\:\mathrm{0}\:\:\:\:\mathrm{5}}\\{\:\:\:\mathrm{0}\:\:\:−\mathrm{5}\:\:\:\mathrm{4}}\end{pmatrix}^{−\mathrm{1}} \begin{pmatrix}{\:\:\:\:\mathrm{2}}\\{−\frac{\mathrm{1}}{\mathrm{4}}}\\{−\frac{\mathrm{2}}{\mathrm{3}}}\end{pmatrix} \\ $$
