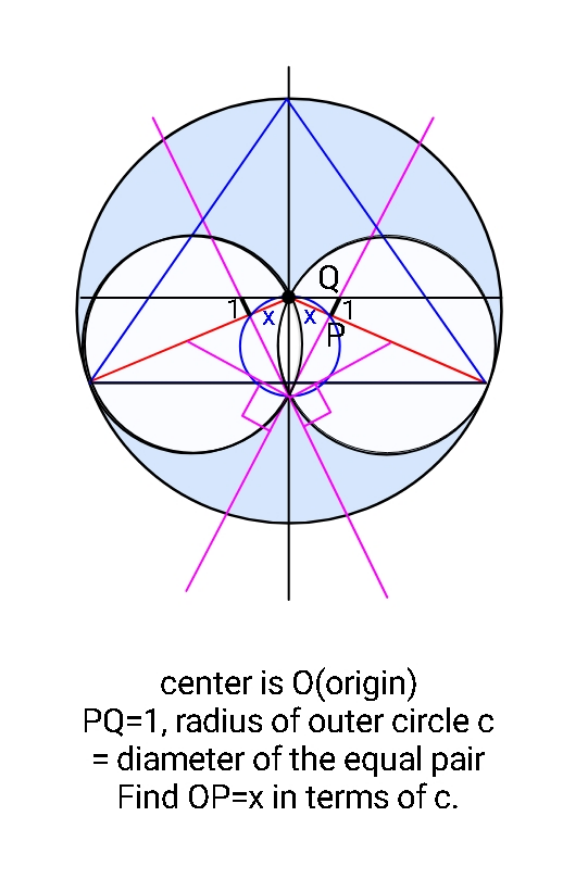
Question Number 156072 by ajfour last updated on 07/Oct/21

Commented by ajfour last updated on 07/Oct/21
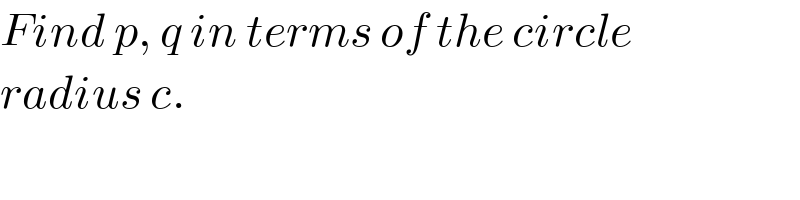
$${Find}\:{p},\:{q}\:{in}\:{terms}\:{of}\:{the}\:{circle} \\ $$$${radius}\:{c}. \\ $$
Commented by mr W last updated on 07/Oct/21

$${you}\:{are}\:{right}\:{sir}! \\ $$
Commented by mr W last updated on 07/Oct/21
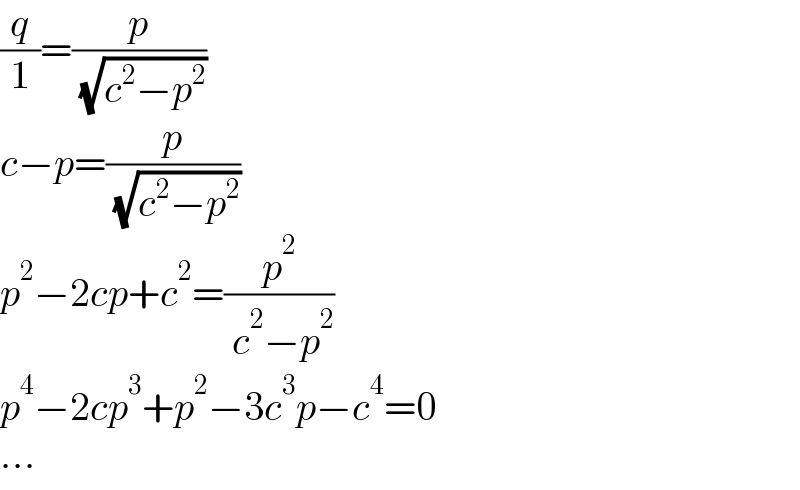
$$\frac{{q}}{\mathrm{1}}=\frac{{p}}{\:\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{2}} }} \\ $$$${c}−{p}=\frac{{p}}{\:\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{2}} }} \\ $$$${p}^{\mathrm{2}} −\mathrm{2}{cp}+{c}^{\mathrm{2}} =\frac{{p}^{\mathrm{2}} }{\:{c}^{\mathrm{2}} −{p}^{\mathrm{2}} } \\ $$$${p}^{\mathrm{4}} −\mathrm{2}{cp}^{\mathrm{3}} +{p}^{\mathrm{2}} −\mathrm{3}{c}^{\mathrm{3}} {p}−{c}^{\mathrm{4}} =\mathrm{0} \\ $$$$… \\ $$
Commented by ajfour last updated on 07/Oct/21
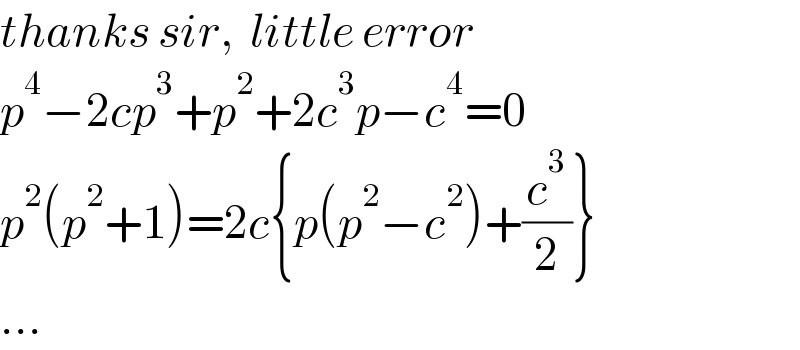
$${thanks}\:{sir},\:\:{little}\:{error} \\ $$$${p}^{\mathrm{4}} −\mathrm{2}{cp}^{\mathrm{3}} +{p}^{\mathrm{2}} +\mathrm{2}{c}^{\mathrm{3}} {p}−{c}^{\mathrm{4}} =\mathrm{0} \\ $$$${p}^{\mathrm{2}} \left({p}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{2}{c}\left\{{p}\left({p}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)+\frac{{c}^{\mathrm{3}} }{\mathrm{2}}\right\} \\ $$$$… \\ $$
Commented by ajfour last updated on 10/Oct/21