Question Number 156137 by cortano last updated on 08/Oct/21
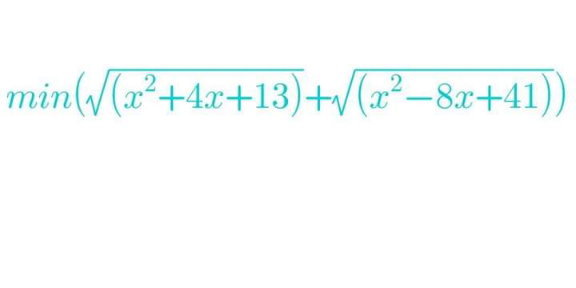
Answered by mr W last updated on 09/Oct/21
Commented by mr W last updated on 09/Oct/21
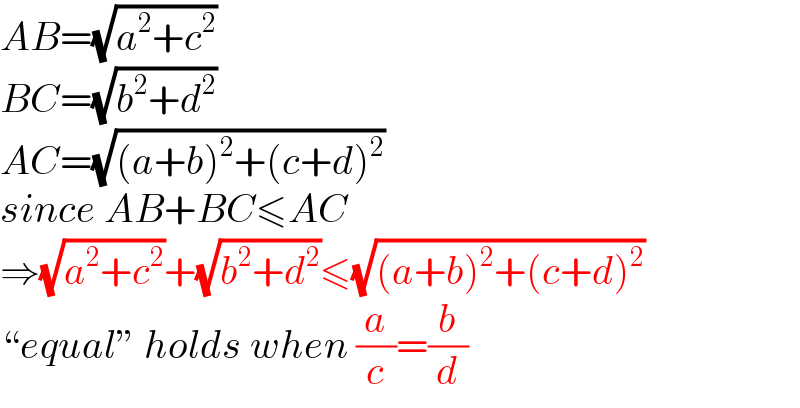
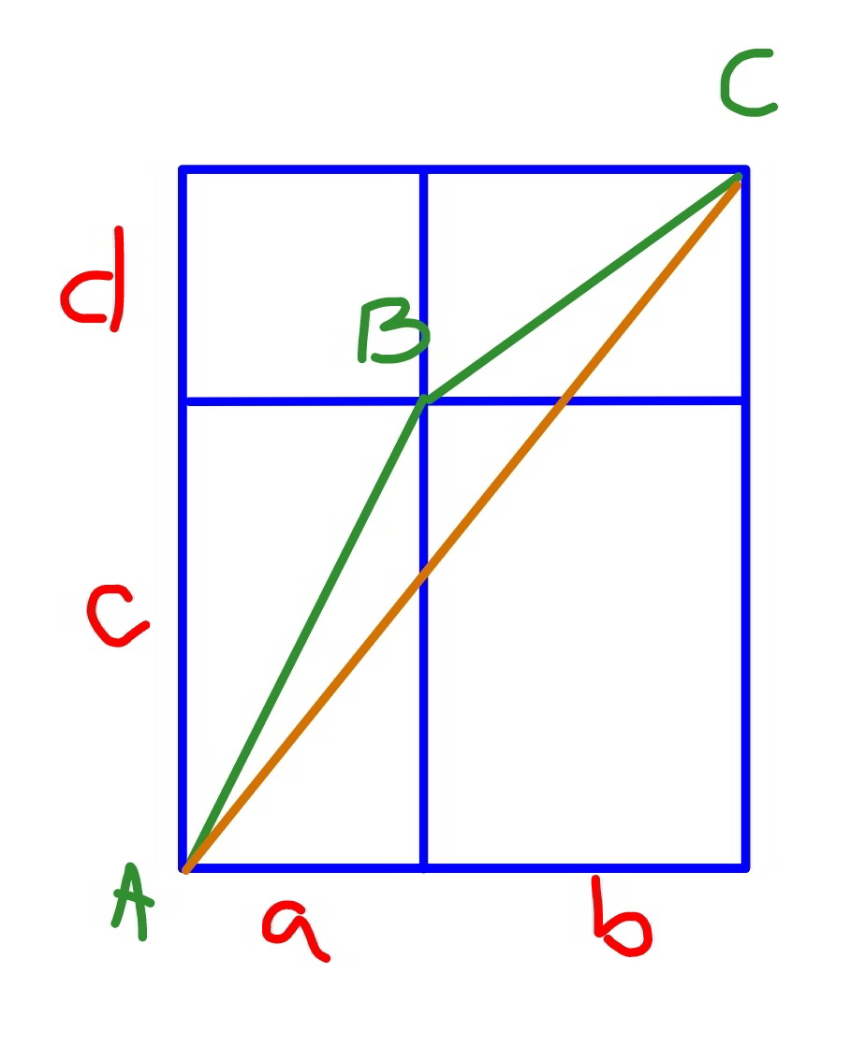
$${AB}=\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$${BC}=\sqrt{{b}^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$$${AC}=\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +\left({c}+{d}\right)^{\mathrm{2}} } \\ $$$${since}\:{AB}+{BC}\leqslant{AC} \\ $$$$\Rightarrow\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} +{d}^{\mathrm{2}} }\leqslant\sqrt{\left({a}+{b}\right)^{\mathrm{2}} +\left({c}+{d}\right)^{\mathrm{2}} } \\ $$$$“{equal}''\:{holds}\:{when}\:\frac{{a}}{{c}}=\frac{{b}}{{d}} \\ $$
Commented by mr W last updated on 09/Oct/21
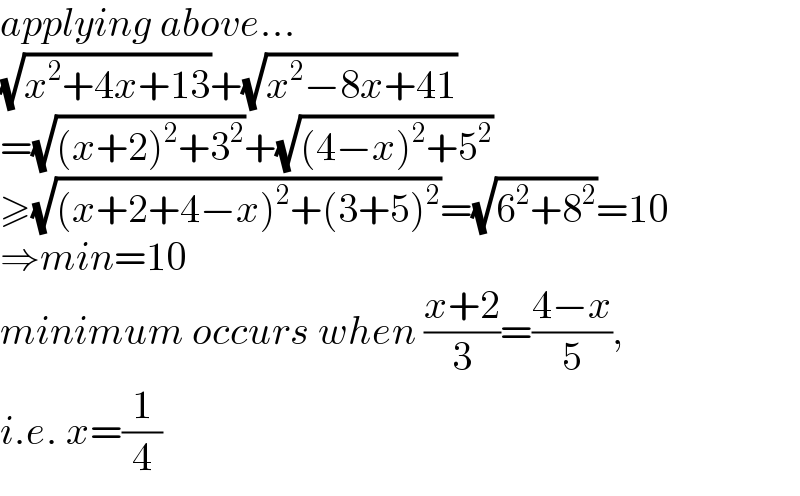
$${applying}\:{above}… \\ $$$$\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{13}}+\sqrt{{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{41}} \\ $$$$=\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }+\sqrt{\left(\mathrm{4}−{x}\right)^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} } \\ $$$$\geqslant\sqrt{\left({x}+\mathrm{2}+\mathrm{4}−{x}\right)^{\mathrm{2}} +\left(\mathrm{3}+\mathrm{5}\right)^{\mathrm{2}} }=\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} }=\mathrm{10} \\ $$$$\Rightarrow{min}=\mathrm{10} \\ $$$${minimum}\:{occurs}\:{when}\:\frac{{x}+\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{4}−{x}}{\mathrm{5}},\: \\ $$$${i}.{e}.\:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by cortano last updated on 10/Oct/21
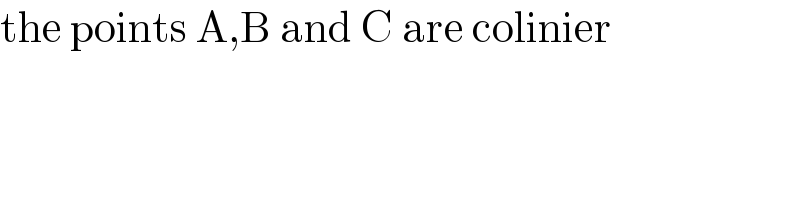
$$\mathrm{the}\:\mathrm{points}\:\mathrm{A},\mathrm{B}\:\mathrm{and}\:\mathrm{C}\:\mathrm{are}\:\mathrm{colinier}\: \\ $$
Commented by cortano last updated on 10/Oct/21
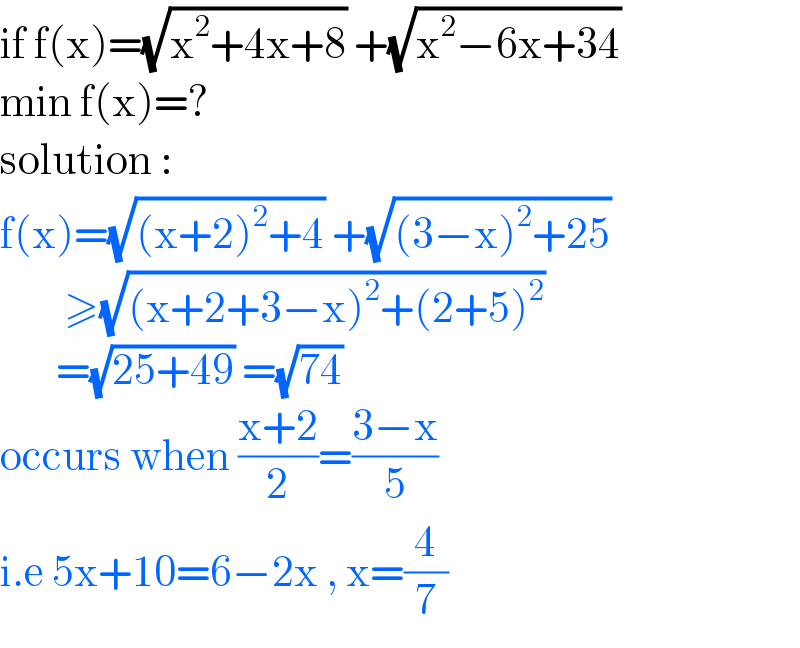
$$\mathrm{if}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{8}}\:+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{34}} \\ $$$$\mathrm{min}\:\mathrm{f}\left(\mathrm{x}\right)=? \\ $$$$\mathrm{solution}\::\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4}}\:+\sqrt{\left(\mathrm{3}−\mathrm{x}\right)^{\mathrm{2}} +\mathrm{25}} \\ $$$$\:\:\:\:\:\:\:\:\geqslant\sqrt{\left(\mathrm{x}+\mathrm{2}+\mathrm{3}−\mathrm{x}\right)^{\mathrm{2}} +\left(\mathrm{2}+\mathrm{5}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:=\sqrt{\mathrm{25}+\mathrm{49}}\:=\sqrt{\mathrm{74}} \\ $$$$\mathrm{occurs}\:\mathrm{when}\:\frac{\mathrm{x}+\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{3}−\mathrm{x}}{\mathrm{5}} \\ $$$$\mathrm{i}.\mathrm{e}\:\mathrm{5x}+\mathrm{10}=\mathrm{6}−\mathrm{2x}\:,\:\mathrm{x}=\frac{\mathrm{4}}{\mathrm{7}} \\ $$
