Question Number 156164 by MathSh last updated on 08/Oct/21

Answered by ghimisi last updated on 09/Oct/21
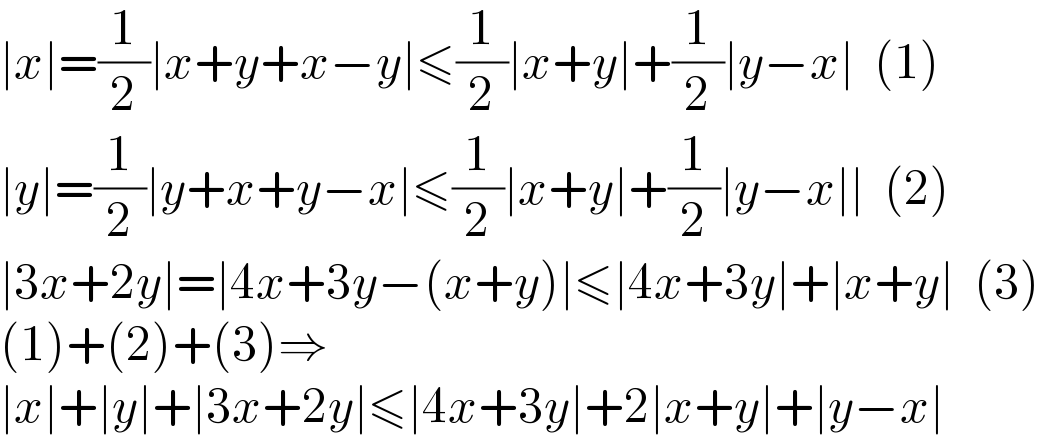
$$\mid{x}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mid{x}+{y}+{x}−{y}\mid\leqslant\frac{\mathrm{1}}{\mathrm{2}}\mid{x}+{y}\mid+\frac{\mathrm{1}}{\mathrm{2}}\mid{y}−{x}\mid\:\:\left(\mathrm{1}\right) \\ $$$$\mid{y}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mid{y}+{x}+{y}−{x}\mid\leqslant\frac{\mathrm{1}}{\mathrm{2}}\mid{x}+{y}\mid+\frac{\mathrm{1}}{\mathrm{2}}\mid{y}−{x}\mid\mid\:\:\left(\mathrm{2}\right) \\ $$$$\mid\mathrm{3}{x}+\mathrm{2}{y}\mid=\mid\mathrm{4}{x}+\mathrm{3}{y}−\left({x}+{y}\right)\mid\leqslant\mid\mathrm{4}{x}+\mathrm{3}{y}\mid+\mid{x}+{y}\mid\:\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)+\left(\mathrm{3}\right)\Rightarrow \\ $$$$\mid{x}\mid+\mid{y}\mid+\mid\mathrm{3}{x}+\mathrm{2}{y}\mid\leqslant\mid\mathrm{4}{x}+\mathrm{3}{y}\mid+\mathrm{2}\mid{x}+{y}\mid+\mid{y}−{x}\mid \\ $$
Commented by MathSh last updated on 09/Oct/21
$$\mathrm{Perfect}\:\mathrm{dear}\:\mathrm{Ser},\:\mathrm{thank}\:\mathrm{you} \\ $$
