Question Number 156176 by MathSh last updated on 08/Oct/21

Answered by ghimisi last updated on 09/Oct/21
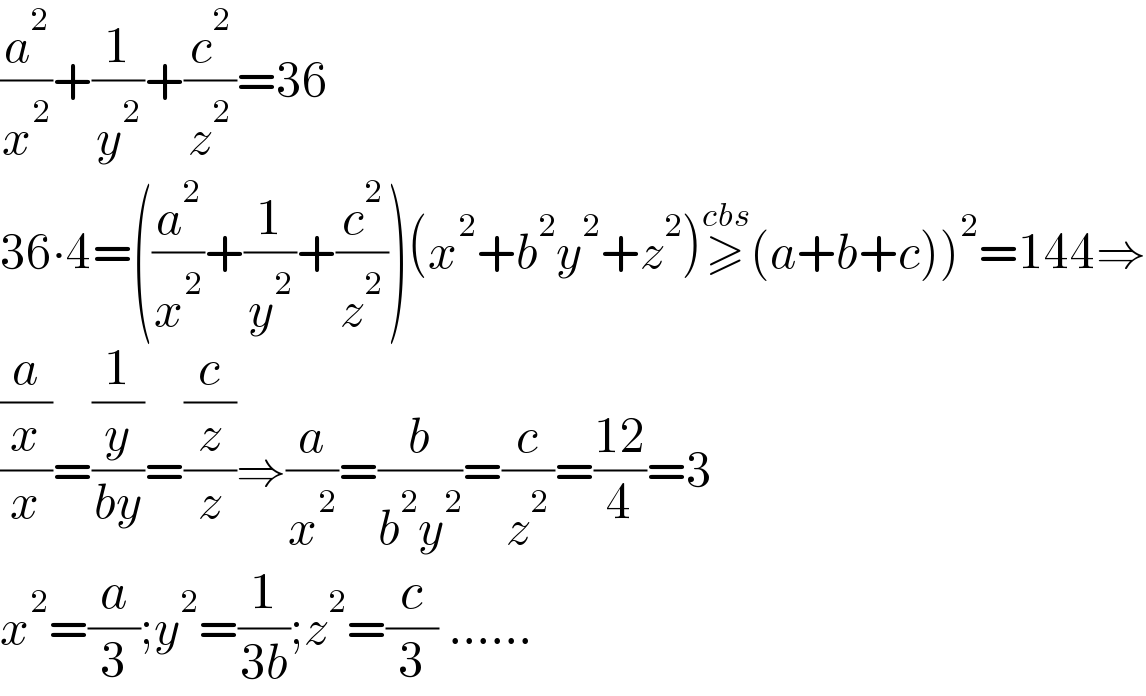
$$\frac{{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{y}^{\mathrm{2}} }+\frac{{c}^{\mathrm{2}} }{{z}^{\mathrm{2}} }=\mathrm{36} \\ $$$$\left.\mathrm{36}\centerdot\mathrm{4}=\left(\frac{{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{y}^{\mathrm{2}} }+\frac{{c}^{\mathrm{2}} }{{z}^{\mathrm{2}} }\right)\left({x}^{\mathrm{2}} +{b}^{\mathrm{2}} {y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)\overset{{cbs}} {\geqslant}\left({a}+{b}+{c}\right)\right)^{\mathrm{2}} =\mathrm{144}\Rightarrow \\ $$$$\frac{\frac{{a}}{{x}}}{{x}}=\frac{\frac{\mathrm{1}}{{y}}}{{by}}=\frac{\frac{{c}}{{z}}}{{z}}\Rightarrow\frac{{a}}{{x}^{\mathrm{2}} }=\frac{{b}}{{b}^{\mathrm{2}} {y}^{\mathrm{2}} }=\frac{{c}}{{z}^{\mathrm{2}} }=\frac{\mathrm{12}}{\mathrm{4}}=\mathrm{3} \\ $$$${x}^{\mathrm{2}} =\frac{{a}}{\mathrm{3}};{y}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}{b}};{z}^{\mathrm{2}} =\frac{{c}}{\mathrm{3}}\:…… \\ $$
Commented by MathSh last updated on 09/Oct/21

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{solution}\:\mathrm{dear}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$
