Question Number 156184 by cortano last updated on 09/Oct/21
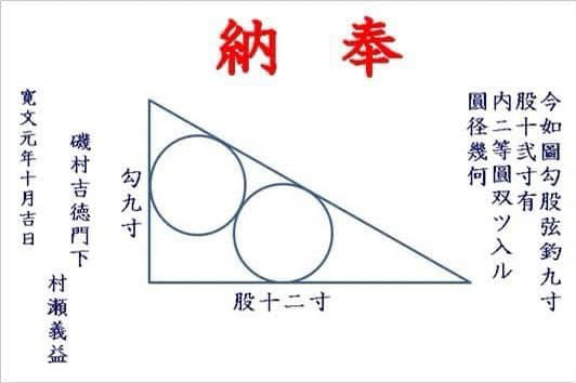
Commented by cortano last updated on 09/Oct/21
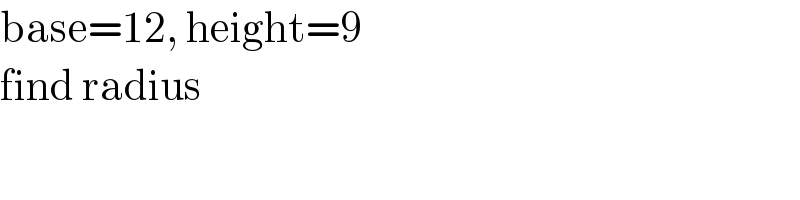
$$\mathrm{base}=\mathrm{12},\:\mathrm{height}=\mathrm{9} \\ $$$$\mathrm{find}\:\mathrm{radius} \\ $$
Answered by mr W last updated on 09/Oct/21
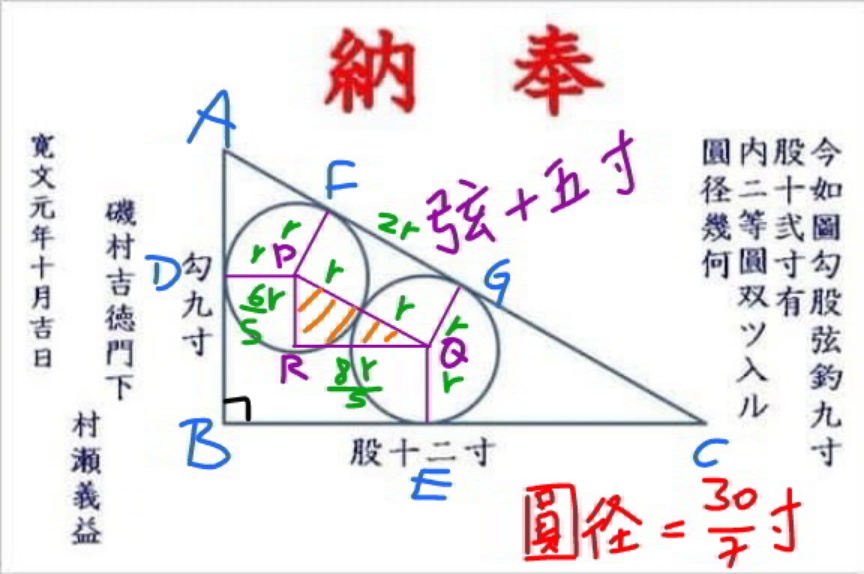
Commented by mr W last updated on 09/Oct/21
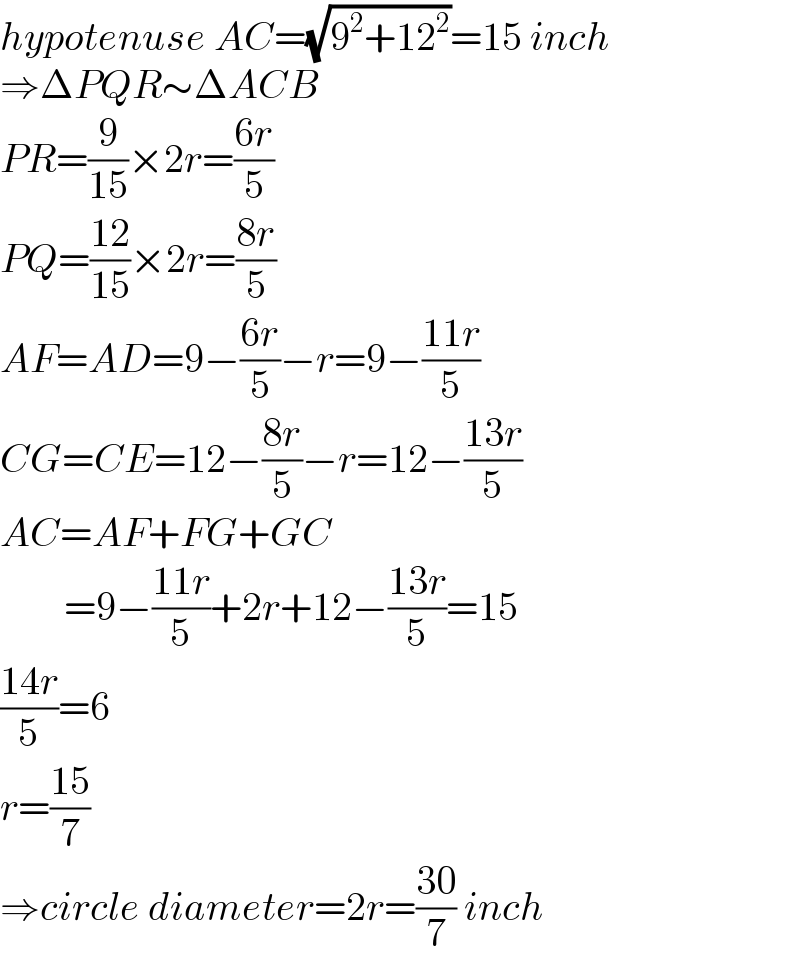
$${hypotenuse}\:{AC}=\sqrt{\mathrm{9}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\mathrm{15}\:{inch} \\ $$$$\Rightarrow\Delta{PQR}\sim\Delta{ACB} \\ $$$${PR}=\frac{\mathrm{9}}{\mathrm{15}}×\mathrm{2}{r}=\frac{\mathrm{6}{r}}{\mathrm{5}} \\ $$$${PQ}=\frac{\mathrm{12}}{\mathrm{15}}×\mathrm{2}{r}=\frac{\mathrm{8}{r}}{\mathrm{5}} \\ $$$${AF}={AD}=\mathrm{9}−\frac{\mathrm{6}{r}}{\mathrm{5}}−{r}=\mathrm{9}−\frac{\mathrm{11}{r}}{\mathrm{5}} \\ $$$${CG}={CE}=\mathrm{12}−\frac{\mathrm{8}{r}}{\mathrm{5}}−{r}=\mathrm{12}−\frac{\mathrm{13}{r}}{\mathrm{5}} \\ $$$${AC}={AF}+{FG}+{GC} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{9}−\frac{\mathrm{11}{r}}{\mathrm{5}}+\mathrm{2}{r}+\mathrm{12}−\frac{\mathrm{13}{r}}{\mathrm{5}}=\mathrm{15} \\ $$$$\frac{\mathrm{14}{r}}{\mathrm{5}}=\mathrm{6} \\ $$$${r}=\frac{\mathrm{15}}{\mathrm{7}} \\ $$$$\Rightarrow{circle}\:{diameter}=\mathrm{2}{r}=\frac{\mathrm{30}}{\mathrm{7}}\:{inch} \\ $$
Commented by cortano last updated on 09/Oct/21
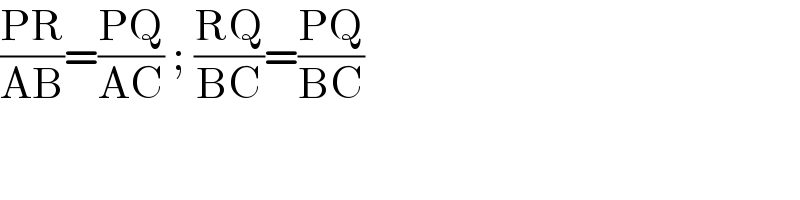
$$\frac{\mathrm{PR}}{\mathrm{AB}}=\frac{\mathrm{PQ}}{\mathrm{AC}}\:;\:\frac{\mathrm{RQ}}{\mathrm{BC}}=\frac{\mathrm{PQ}}{\mathrm{BC}} \\ $$
Commented by Tawa11 last updated on 10/Oct/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by nikif99 last updated on 09/Oct/21

