Question-156186

Question Number 156186 by DavidSmath last updated on 09/Oct/21

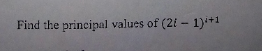
Commented by DavidSmath last updated on 09/Oct/21

$$\mathrm{show}\:\mathrm{clear}\:\mathrm{workings}… \\ $$

Commented by MJS_new last updated on 09/Oct/21

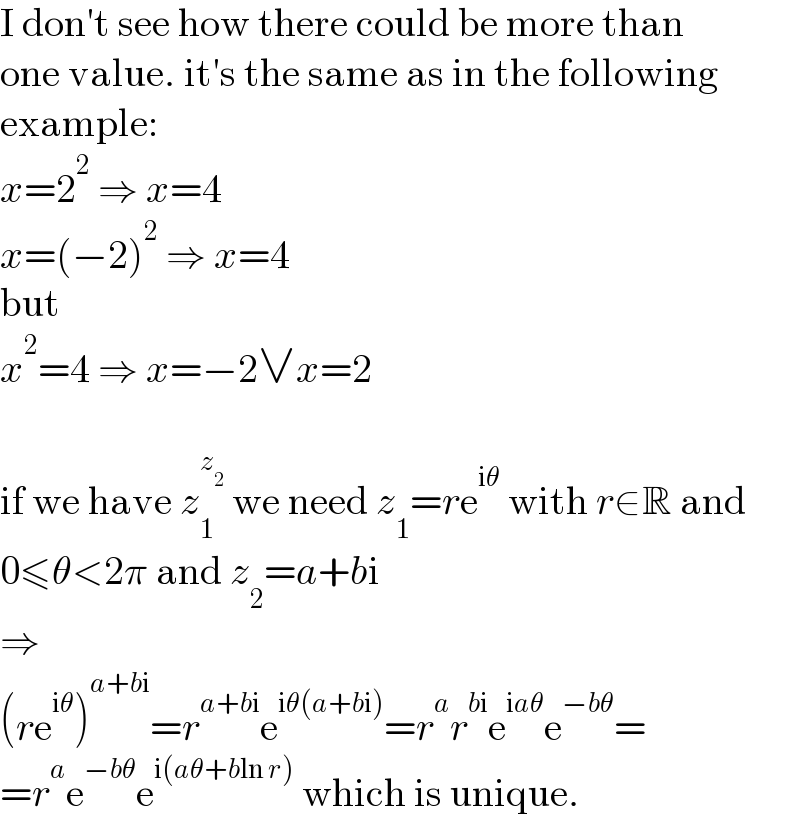
I don′t see how there could be more than one value. it′s the same as in the following example: x=2^2 ⇒ x=4 x=(−2)^2 ⇒ x=4 but x^2 =4 ⇒ x=−2∨x=2 if we have z_1 ^z_2 we need z_1 =re^(iθ) with r∈R and 0≤θ<2π and z_2 =a+bi ⇒ (re^(iθ) )^(a+bi) =r^(a+bi) e^(iθ(a+bi)) =r^a r^(bi) e^(iaθ) e^(−bθ) = =r^a e^(−bθ) e^(i(aθ+bln r)) which is unique.

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{see}\:\mathrm{how}\:\mathrm{there}\:\mathrm{could}\:\mathrm{be}\:\mathrm{more}\:\mathrm{than} \\ $$$$\mathrm{one}\:\mathrm{value}.\:\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{in}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{example}: \\ $$$${x}=\mathrm{2}^{\mathrm{2}} \:\Rightarrow\:{x}=\mathrm{4} \\ $$$${x}=\left(−\mathrm{2}\right)^{\mathrm{2}} \:\Rightarrow\:{x}=\mathrm{4} \\ $$$$\mathrm{but} \\ $$$${x}^{\mathrm{2}} =\mathrm{4}\:\Rightarrow\:{x}=−\mathrm{2}\vee{x}=\mathrm{2} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{have}\:{z}_{\mathrm{1}} ^{{z}_{\mathrm{2}} } \:\mathrm{we}\:\mathrm{need}\:{z}_{\mathrm{1}} ={r}\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{with}\:{r}\in\mathbb{R}\:\mathrm{and} \\ $$$$\mathrm{0}\leqslant\theta<\mathrm{2}\pi\:\mathrm{and}\:{z}_{\mathrm{2}} ={a}+{b}\mathrm{i} \\ $$$$\Rightarrow \\ $$$$\left({r}\mathrm{e}^{\mathrm{i}\theta} \right)^{{a}+{b}\mathrm{i}} ={r}^{{a}+{b}\mathrm{i}} \mathrm{e}^{\mathrm{i}\theta\left({a}+{b}\mathrm{i}\right)} ={r}^{{a}} {r}^{{b}\mathrm{i}} \mathrm{e}^{\mathrm{i}{a}\theta} \mathrm{e}^{−{b}\theta} = \\ $$$$={r}^{{a}} \mathrm{e}^{−{b}\theta} \mathrm{e}^{\mathrm{i}\left({a}\theta+{b}\mathrm{ln}\:{r}\right)} \:\mathrm{which}\:\mathrm{is}\:\mathrm{unique}. \\ $$

Answered by mr W last updated on 09/Oct/21

z=(2i−1)^(i+1) =[(√5)e^((π−tan^(−1) 2)i) ]^(i+1) =(√5)e^(−π+tan^(−1) 2) [(√5)e^((π−tan^(−1) 2)) ]^i =(√5)e^(−π+tan^(−1) 2) e^((π−tan^(−1) 2+ln (√5))i) it′s principal value is Arg(z)=π−tan^(−1) 2+ln (√5)≈2.839

$${z}=\left(\mathrm{2}{i}−\mathrm{1}\right)^{{i}+\mathrm{1}} =\left[\sqrt{\mathrm{5}}{e}^{\left(\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\right){i}} \right]^{{i}+\mathrm{1}} \\ $$$$=\sqrt{\mathrm{5}}{e}^{−\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{2}} \left[\sqrt{\mathrm{5}}{e}^{\left(\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\right)} \right]^{{i}} \\ $$$$=\sqrt{\mathrm{5}}{e}^{−\pi+\mathrm{tan}^{−\mathrm{1}} \mathrm{2}} {e}^{\left(\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{ln}\:\sqrt{\mathrm{5}}\right){i}} \\ $$$${it}'{s}\:{principal}\:{value}\:{is} \\ $$$${Arg}\left({z}\right)=\pi−\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{ln}\:\sqrt{\mathrm{5}}\approx\mathrm{2}.\mathrm{839} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply