Menu Close

Question-156316

Tinku Tara 0 Comments
Pin




Question Number 156316 by cortano last updated on 10/Oct/21
Commented by cortano last updated on 10/Oct/21
AD=DE=EB , AF : FG : GC=1:2:1 what fraction of ΔABC is shaded?
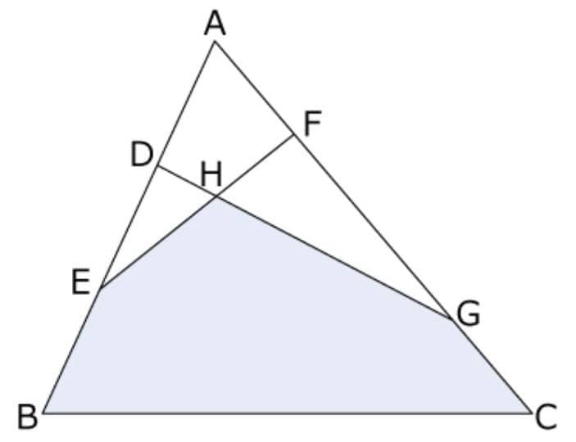
$$\mathrm{AD}=\mathrm{DE}=\mathrm{EB}\:,\:\mathrm{AF}\::\:\mathrm{FG}\::\:\mathrm{GC}=\mathrm{1}:\mathrm{2}:\mathrm{1} \\ $$$$\:\mathrm{what}\:\mathrm{fraction}\:\mathrm{of}\:\Delta\mathrm{ABC}\:\mathrm{is}\:\mathrm{shaded}? \\ $$
Answered by mr W last updated on 10/Oct/21
Commented by mr W last updated on 10/Oct/21
say area of ΔABC is A. ((CG)/(AC))=(1/4) ⇒(A_1 /A)=(1/4) ((ΔBGA)/A)=(3/4) ((BE)/(BA))=(1/3) ⇒(A_2 /(ΔBGA))=(1/3) ⇒(A_2 /A)=(1/3)×(3/4)=(1/4) ((ΔGEA)/(ΔBGA))=(2/3) ⇒((ΔGEA)/A)=(2/3)×(3/4)=(1/2) ((ED)/(EA))=(1/2) ⇒((ΔGED)/(ΔGEA))=(1/2) ⇒((ΔGED)/A)=(1/2)×(1/2)=(1/4) ((KF)/(AF))=((DE)/(AE))=(1/2), ((AF)/(FG))=(1/2) ⇒((KF)/(FG))=(1/2)×(1/2)=(1/4) ((DH)/(HG))=((KF)/(FG))=(1/4) ⇒((HG)/(DG))=(4/(1+4))=(4/5) ⇒(A_3 /(ΔGED))=(4/5) ⇒(A_3 /A)=(4/5)×(1/4)=(1/5) ((shaded)/(ΔABC))=((A_1 +A_2 +A_3 )/A)=(1/4)+(1/4)+(1/5)=(7/(10))
$${say}\:{area}\:{of}\:\Delta{ABC}\:{is}\:{A}. \\ $$$$\frac{{CG}}{{AC}}=\frac{\mathrm{1}}{\mathrm{4}}\: \\ $$$$\Rightarrow\frac{{A}_{\mathrm{1}} }{{A}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\Delta{BGA}}{{A}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{{BE}}{{BA}}=\frac{\mathrm{1}}{\mathrm{3}}\: \\ $$$$\Rightarrow\frac{{A}_{\mathrm{2}} }{\Delta{BGA}}=\frac{\mathrm{1}}{\mathrm{3}}\: \\ $$$$\Rightarrow\frac{{A}_{\mathrm{2}} }{{A}}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\Delta{GEA}}{\Delta{BGA}}=\frac{\mathrm{2}}{\mathrm{3}}\: \\ $$$$\Rightarrow\frac{\Delta{GEA}}{{A}}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{ED}}{{EA}}=\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\Rightarrow\frac{\Delta{GED}}{\Delta{GEA}}=\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\Rightarrow\frac{\Delta{GED}}{{A}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{{KF}}{{AF}}=\frac{{DE}}{{AE}}=\frac{\mathrm{1}}{\mathrm{2}},\:\frac{{AF}}{{FG}}=\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\Rightarrow\frac{{KF}}{{FG}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{{DH}}{{HG}}=\frac{{KF}}{{FG}}=\frac{\mathrm{1}}{\mathrm{4}}\: \\ $$$$\Rightarrow\frac{{HG}}{{DG}}=\frac{\mathrm{4}}{\mathrm{1}+\mathrm{4}}=\frac{\mathrm{4}}{\mathrm{5}}\: \\ $$$$\Rightarrow\frac{{A}_{\mathrm{3}} }{\Delta{GED}}=\frac{\mathrm{4}}{\mathrm{5}}\: \\ $$$$\Rightarrow\frac{{A}_{\mathrm{3}} }{{A}}=\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$ \\ $$$$\frac{{shaded}}{\Delta{ABC}}=\frac{{A}_{\mathrm{1}} +{A}_{\mathrm{2}} +{A}_{\mathrm{3}} }{{A}}=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{7}}{\mathrm{10}} \\ $$
Commented by Tawa11 last updated on 10/Oct/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by otchereabdullai@gmail.com last updated on 10/Oct/21
Brilliant !
$$\mathrm{Brilliant}\:! \\ $$
Answered by ajfour last updated on 10/Oct/21
AB=3b AC=4c s=△_(ABC) =6(b×c) △_(AEF) =(b×c) △_(ADG) =(3/2)(b×c) p=△_(AEF) +△_(ADG) =(5/2)(b×c) for H_(−) eq. of DG: h= b+λ(2c−b) eq. of FE: h= c+μ(3b−c) comparing coefficients of a,b 1−λ=3μ & 1−μ=2λ ⇒ 1−μ=2(1−3μ) ⇒ μ=(1/5) , λ=(2/5) h=b+(2/5)(2c−b)=((3b+4c)/5) △_(DAH) =(1/2)b×(((3b+4c)/5)) △_(HAF) =(1/2)(((3b+4c)/5))×c adding =(1/2)(b−c)(((3b+4c)/5)) q=(△_(DAH) +△_(HAF) ) =((7(b×c))/(10)) shaded area =△_(ABC) −{△_(AEF) +△_(AEG) −(△_(DAH) +△_(HAF) )} shaded area=s−(p−q) ((shaded area)/△_(ABC) )=((s−p+q)/s) ((shaded area)/△_(ABC) )=((6−(5/2)+(7/(10)))/6) ((shaded area)/△_(ABC) ) =((42)/(60))=(7/(10)) ✓
$$\mathrm{AB}=\mathrm{3b}\:\:\:\:\:\mathrm{AC}=\mathrm{4c} \\ $$$$\mathrm{s}=\bigtriangleup_{\mathrm{ABC}} =\mathrm{6}\left(\mathrm{b}×\mathrm{c}\right) \\ $$$$\bigtriangleup_{\mathrm{AEF}} =\left(\mathrm{b}×\mathrm{c}\right) \\ $$$$\bigtriangleup_{\mathrm{ADG}} =\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{b}×\mathrm{c}\right) \\ $$$$\mathrm{p}=\bigtriangleup_{\mathrm{AEF}} +\bigtriangleup_{\mathrm{ADG}} =\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{b}×\mathrm{c}\right) \\ $$$$\underset{−} {\mathrm{for}\:\mathrm{H}}\: \\ $$$$\:\mathrm{eq}.\:\mathrm{of}\:\mathrm{DG}:\:\:\mathrm{h}=\:\mathrm{b}+\lambda\left(\mathrm{2c}−\mathrm{b}\right) \\ $$$$\:\mathrm{eq}.\:\mathrm{of}\:\:\mathrm{FE}:\:\:\:\mathrm{h}=\:\mathrm{c}+\mu\left(\mathrm{3b}−\mathrm{c}\right) \\ $$$$\mathrm{comparing}\:\mathrm{coefficients}\:\mathrm{of}\:\mathrm{a},\mathrm{b} \\ $$$$\mathrm{1}−\lambda=\mathrm{3}\mu\:\:\&\:\:\:\mathrm{1}−\mu=\mathrm{2}\lambda \\ $$$$\Rightarrow\:\:\mathrm{1}−\mu=\mathrm{2}\left(\mathrm{1}−\mathrm{3}\mu\right) \\ $$$$\Rightarrow\:\:\mu=\frac{\mathrm{1}}{\mathrm{5}}\:\:,\:\:\lambda=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\mathrm{h}=\mathrm{b}+\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{2c}−\mathrm{b}\right)=\frac{\mathrm{3b}+\mathrm{4c}}{\mathrm{5}} \\ $$$$\bigtriangleup_{\mathrm{DAH}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{b}×\left(\frac{\mathrm{3b}+\mathrm{4c}}{\mathrm{5}}\right) \\ $$$$\bigtriangleup_{\mathrm{HAF}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3b}+\mathrm{4c}}{\mathrm{5}}\right)×\mathrm{c} \\ $$$$\mathrm{adding}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{b}−\mathrm{c}\right)\left(\frac{\mathrm{3b}+\mathrm{4c}}{\mathrm{5}}\right) \\ $$$$\:\mathrm{q}=\left(\bigtriangleup_{\mathrm{DAH}} +\bigtriangleup_{\mathrm{HAF}} \right)\:\:=\frac{\mathrm{7}\left(\mathrm{b}×\mathrm{c}\right)}{\mathrm{10}} \\ $$$$\mathrm{shaded}\:\mathrm{area} \\ $$$$\:=\bigtriangleup_{\mathrm{ABC}} −\left\{\bigtriangleup_{\mathrm{AEF}} +\bigtriangleup_{\mathrm{AEG}} −\left(\bigtriangleup_{\mathrm{DAH}} +\bigtriangleup_{\mathrm{HAF}} \right)\right\} \\ $$$$\mathrm{shaded}\:\mathrm{area}=\mathrm{s}−\left(\mathrm{p}−\mathrm{q}\right) \\ $$$$\frac{\mathrm{shaded}\:\mathrm{area}}{\bigtriangleup_{\mathrm{ABC}} }=\frac{\mathrm{s}−\mathrm{p}+\mathrm{q}}{\mathrm{s}} \\ $$$$\frac{\mathrm{shaded}\:\mathrm{area}}{\bigtriangleup_{\mathrm{ABC}} }=\frac{\mathrm{6}−\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{7}}{\mathrm{10}}}{\mathrm{6}} \\ $$$$\:\:\:\:\frac{\mathrm{shaded}\:\mathrm{area}}{\bigtriangleup_{\mathrm{ABC}} }\:\:\:\:\:\:=\frac{\mathrm{42}}{\mathrm{60}}=\frac{\mathrm{7}}{\mathrm{10}}\:\:\checkmark \\ $$$$ \\ $$
Commented by mr W last updated on 10/Oct/21
great!
$${great}! \\ $$
Answered by john_santu last updated on 11/Oct/21
by length ratio of triangles (1) ((area ΔAEG)/(area ΔABC)) = (((2/3)×(3/4))/1)=((1/2)/1) (2) ((area shaded)/(area ΔABC))=(((1/2)(((1+2)/(1+2+2))))/1)=(3/(10)) (3) fraction of area =1−(3/(10))=(7/(10))
$${by}\:{length}\:{ratio}\:{of}\:{triangles} \\ $$$$\left(\mathrm{1}\right)\:\frac{{area}\:\Delta{AEG}}{{area}\:\Delta{ABC}}\:=\:\frac{\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{4}}}{\mathrm{1}}=\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}} \\ $$$$\left(\mathrm{2}\right)\:\frac{{area}\:{shaded}}{{area}\:\Delta{ABC}}=\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}+\mathrm{2}}{\mathrm{1}+\mathrm{2}+\mathrm{2}}\right)}{\mathrm{1}}=\frac{\mathrm{3}}{\mathrm{10}} \\ $$$$\left(\mathrm{3}\right)\:{fraction}\:{of}\:{area}\:=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{10}}=\frac{\mathrm{7}}{\mathrm{10}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *