Question-156333

Question Number 156333 by MathSh last updated on 10/Oct/21

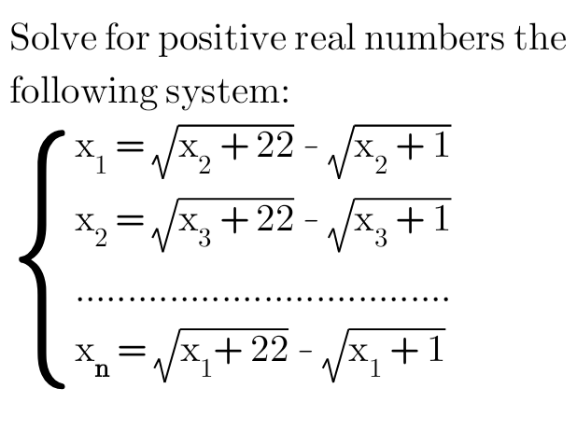
Answered by Rasheed.Sindhi last updated on 10/Oct/21

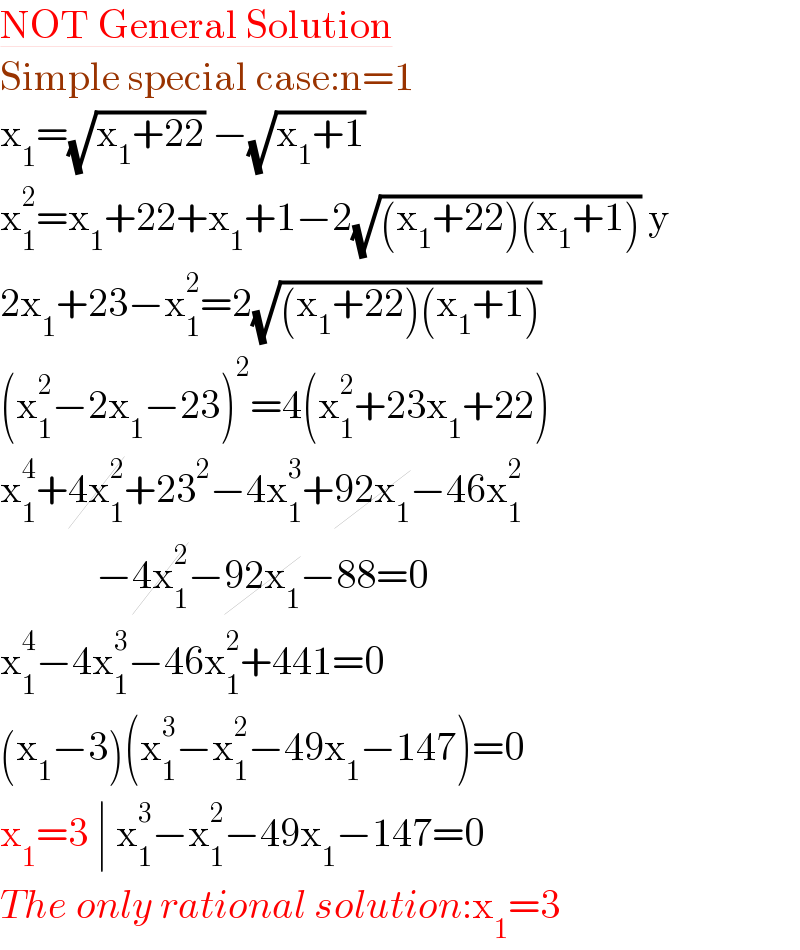
NOT General Solution Simple special case:n=1 x_1 =(√(x_1 +22)) −(√(x_1 +1)) x_1 ^2 =x_1 +22+x_1 +1−2(√((x_1 +22)(x_1 +1))) y 2x_1 +23−x_1 ^2 =2(√((x_1 +22)(x_1 +1))) (x_1 ^2 −2x_1 −23)^2 =4(x_1 ^2 +23x_1 +22) x_1 ^4 +4x_1 ^2 +23^2 −4x_1 ^3 +92x_1 −46x_1 ^2 −4x_1 ^2 −92x_1 −88=0 x_1 ^4 −4x_1 ^3 −46x_1 ^2 +441=0 (x_1 −3)(x_1 ^3 −x_1 ^2 −49x_1 −147)=0 x_1 =3 ∣ x_1 ^3 −x_1 ^2 −49x_1 −147=0 The only rational solution:x_1 =3

$$\underline{\mathrm{NOT}\:\mathrm{General}\:\mathrm{Solution}} \\ $$$$\mathrm{Simple}\:\mathrm{special}\:\mathrm{case}:\mathrm{n}=\mathrm{1} \\ $$$$\mathrm{x}_{\mathrm{1}} =\sqrt{\mathrm{x}_{\mathrm{1}} +\mathrm{22}}\:−\sqrt{\mathrm{x}_{\mathrm{1}} +\mathrm{1}}\: \\ $$$$\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{x}_{\mathrm{1}} +\mathrm{22}+\mathrm{x}_{\mathrm{1}} +\mathrm{1}−\mathrm{2}\sqrt{\left(\mathrm{x}_{\mathrm{1}} +\mathrm{22}\right)\left(\mathrm{x}_{\mathrm{1}} +\mathrm{1}\right)}\:\mathrm{y} \\ $$$$\mathrm{2x}_{\mathrm{1}} +\mathrm{23}−\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{2}\sqrt{\left(\mathrm{x}_{\mathrm{1}} +\mathrm{22}\right)\left(\mathrm{x}_{\mathrm{1}} +\mathrm{1}\right)}\: \\ $$$$\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2x}_{\mathrm{1}} −\mathrm{23}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{23x}_{\mathrm{1}} +\mathrm{22}\right) \\ $$$$\mathrm{x}_{\mathrm{1}} ^{\mathrm{4}} +\cancel{\mathrm{4x}_{\mathrm{1}} ^{\mathrm{2}} }+\mathrm{23}^{\mathrm{2}} −\mathrm{4x}_{\mathrm{1}} ^{\mathrm{3}} +\cancel{\mathrm{92x}_{\mathrm{1}} }−\mathrm{46x}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\cancel{\mathrm{4x}_{\mathrm{1}} ^{\mathrm{2}} }−\cancel{\mathrm{92x}_{\mathrm{1}} }−\mathrm{88}=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1}} ^{\mathrm{4}} −\mathrm{4x}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{46x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{441}=\mathrm{0} \\ $$$$\left(\mathrm{x}_{\mathrm{1}} −\mathrm{3}\right)\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{49x}_{\mathrm{1}} −\mathrm{147}\right)=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1}} =\mathrm{3}\:\mid\:\mathrm{x}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{49x}_{\mathrm{1}} −\mathrm{147}=\mathrm{0} \\ $$$${The}\:{only}\:{rational}\:{solution}:\mathrm{x}_{\mathrm{1}} =\mathrm{3} \\ $$

Commented by MathSh last updated on 10/Oct/21

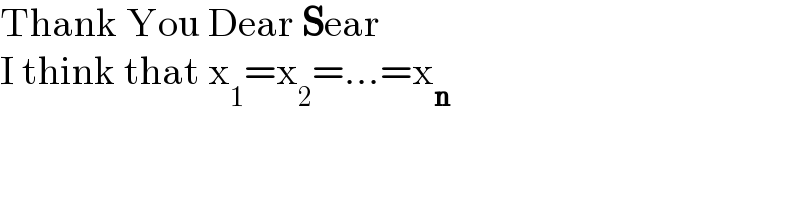
Thank You Dear Sear I think that x_1 =x_2 =...=x_n

$$\mathrm{Thank}\:\mathrm{You}\:\mathrm{Dear}\:\boldsymbol{\mathrm{S}}\mathrm{ear} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{x}_{\mathrm{1}} =\mathrm{x}_{\mathrm{2}} =…=\mathrm{x}_{\boldsymbol{\mathrm{n}}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply