Question Number 156422 by SANOGO last updated on 11/Oct/21
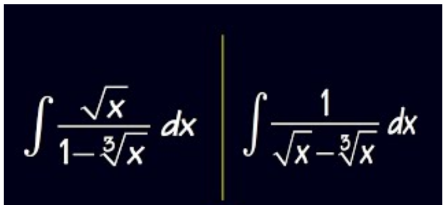
Commented by cortano last updated on 11/Oct/21
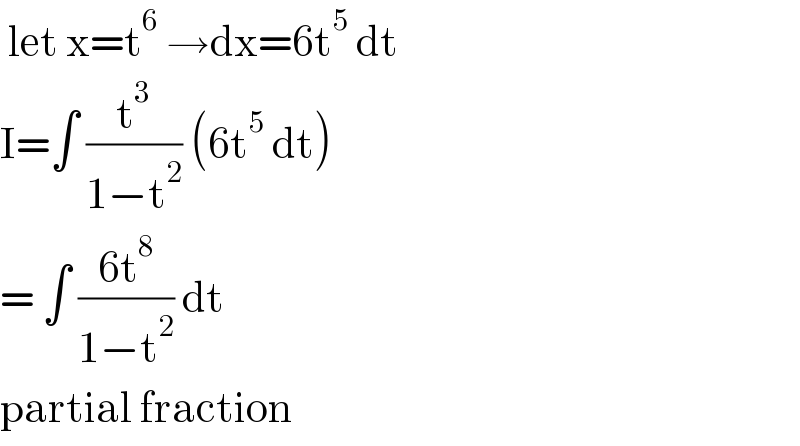
$$\:\mathrm{let}\:\mathrm{x}=\mathrm{t}^{\mathrm{6}} \:\rightarrow\mathrm{dx}=\mathrm{6t}^{\mathrm{5}} \:\mathrm{dt} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:\left(\mathrm{6t}^{\mathrm{5}} \:\mathrm{dt}\right) \\ $$$$=\:\int\:\frac{\mathrm{6t}^{\mathrm{8}} }{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\: \\ $$$$\mathrm{partial}\:\mathrm{fraction} \\ $$
Commented by SANOGO last updated on 11/Oct/21

$${merci}\:{bien} \\ $$
Answered by puissant last updated on 11/Oct/21
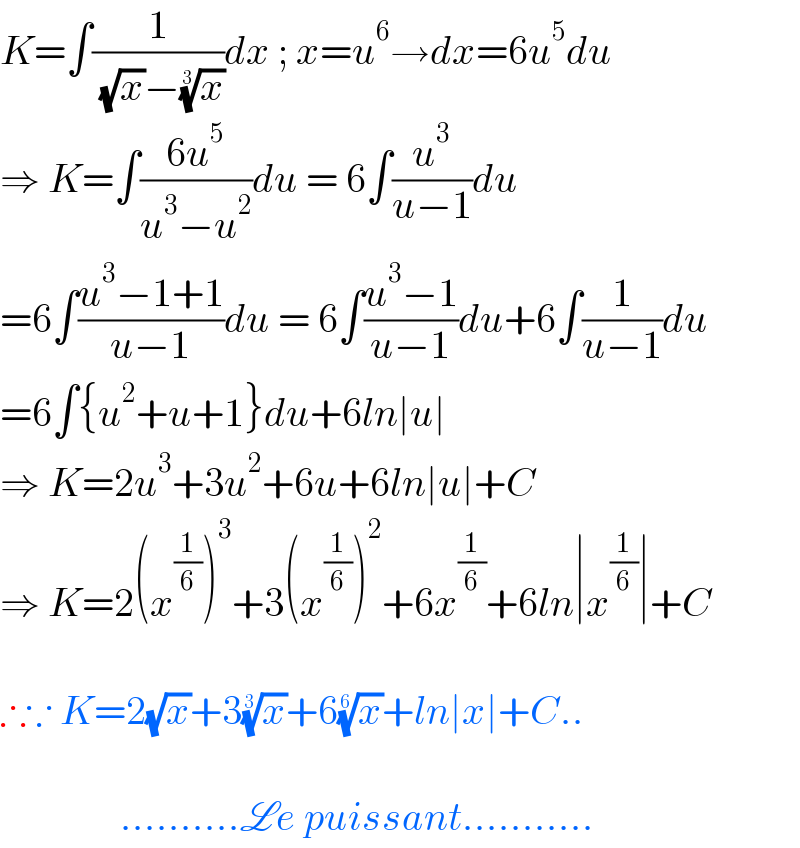
$${K}=\int\frac{\mathrm{1}}{\:\sqrt{{x}}−\sqrt[{\mathrm{3}}]{{x}}}{dx}\:;\:{x}={u}^{\mathrm{6}} \rightarrow{dx}=\mathrm{6}{u}^{\mathrm{5}} {du} \\ $$$$\Rightarrow\:{K}=\int\frac{\mathrm{6}{u}^{\mathrm{5}} }{{u}^{\mathrm{3}} −{u}^{\mathrm{2}} }{du}\:=\:\mathrm{6}\int\frac{{u}^{\mathrm{3}} }{{u}−\mathrm{1}}{du} \\ $$$$=\mathrm{6}\int\frac{{u}^{\mathrm{3}} −\mathrm{1}+\mathrm{1}}{{u}−\mathrm{1}}{du}\:=\:\mathrm{6}\int\frac{{u}^{\mathrm{3}} −\mathrm{1}}{{u}−\mathrm{1}}{du}+\mathrm{6}\int\frac{\mathrm{1}}{{u}−\mathrm{1}}{du} \\ $$$$=\mathrm{6}\int\left\{{u}^{\mathrm{2}} +{u}+\mathrm{1}\right\}{du}+\mathrm{6}{ln}\mid{u}\mid \\ $$$$\Rightarrow\:{K}=\mathrm{2}{u}^{\mathrm{3}} +\mathrm{3}{u}^{\mathrm{2}} +\mathrm{6}{u}+\mathrm{6}{ln}\mid{u}\mid+{C} \\ $$$$\Rightarrow\:{K}=\mathrm{2}\left({x}^{\frac{\mathrm{1}}{\mathrm{6}}} \right)^{\mathrm{3}} +\mathrm{3}\left({x}^{\frac{\mathrm{1}}{\mathrm{6}}} \right)^{\mathrm{2}} +\mathrm{6}{x}^{\frac{\mathrm{1}}{\mathrm{6}}} +\mathrm{6}{ln}\mid{x}^{\frac{\mathrm{1}}{\mathrm{6}}} \mid+{C} \\ $$$$ \\ $$$$\therefore\because\:{K}=\mathrm{2}\sqrt{{x}}+\mathrm{3}\sqrt[{\mathrm{3}}]{{x}}+\mathrm{6}\sqrt[{\mathrm{6}}]{{x}}+{ln}\mid{x}\mid+{C}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……….\mathscr{L}{e}\:{puissant}……….. \\ $$
Commented by SANOGO last updated on 11/Oct/21

$${merci}\:{bien} \\ $$
