Question Number 156508 by cortano last updated on 12/Oct/21
Answered by JDamian last updated on 12/Oct/21

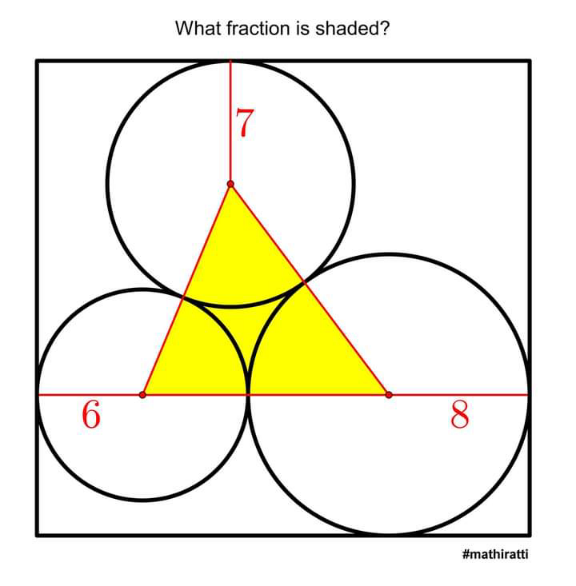
$$\frac{{A}_{{triangle}} }{{A}_{\boldsymbol{{rectangle}}} }\:? \\ $$$${A}_{{triangle}} =\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$${a}=\mathrm{6}+\mathrm{7}=\mathrm{13} \\ $$$${b}=\mathrm{7}+\mathrm{8}=\mathrm{15} \\ $$$${c}=\mathrm{6}+\mathrm{8}=\mathrm{14} \\ $$$${s}=\frac{{a}+{b}+{c}}{\mathrm{2}}=\frac{\mathrm{42}}{\mathrm{2}}=\mathrm{21} \\ $$$${A}_{{triangle}} =\sqrt{\mathrm{21}\left(\mathrm{21}−\mathrm{13}\right)\left(\mathrm{21}−\mathrm{15}\right)\left(\mathrm{21}−\mathrm{14}\right)}= \\ $$$$=\sqrt{\mathrm{21}×\mathrm{8}×\mathrm{6}×\mathrm{7}}=\mathrm{84} \\ $$$${A}_{\boldsymbol{{rectangle}}} =\:{width}\:×\:{height}\:= \\ $$$$=\:\mathrm{28}\:×\:\left(\mathrm{7}+\mathrm{8}+{h}_{{triangle}} \right) \\ $$$${A}_{{triangle}} =\frac{\mathrm{14}×{h}_{{triangle}} }{\mathrm{2}}=\mathrm{84} \\ $$$${h}_{{triangle}} =\frac{\mathrm{2}×\mathrm{84}}{\mathrm{14}}=\mathrm{12} \\ $$$${A}_{\boldsymbol{{rectangle}}} =\:\mathrm{28}×\left(\mathrm{7}+\mathrm{8}+\mathrm{12}\right)=\mathrm{28}×\mathrm{27} \\ $$$$\frac{{A}_{{triangle}} }{{A}_{\boldsymbol{{rectangle}}} }\:=\frac{\mathrm{84}}{\mathrm{28}×\mathrm{27}}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$
Commented by cortano last updated on 12/Oct/21

$$\mathrm{wrong}.\:\mathrm{it}\:\frac{\mathrm{84}}{\mathrm{756}}\:=\:\frac{\mathrm{1}}{\mathrm{9}} \\ $$
Commented by JDamian last updated on 12/Oct/21
is it not a square?
Oops, I see now it is not a square.
Commented by Tawa11 last updated on 12/Oct/21

$$\mathrm{great}\:\mathrm{sir}. \\ $$
