Menu Close

Question-156509

Tinku Tara 0 Comments
Pin




Question Number 156509 by ARUNG_Brandon_MBU last updated on 12/Oct/21
Commented by mr W last updated on 12/Oct/21
both squares are of equal size?
$${both}\:{squares}\:{are}\:{of}\:{equal}\:{size}? \\ $$
Commented by ARUNG_Brandon_MBU last updated on 12/Oct/21
I don′t really know Sir. I think so too
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{really}\:\mathrm{know}\:\mathrm{Sir}.\:\mathrm{I}\:\mathrm{think}\:\mathrm{so}\:\mathrm{too} \\ $$
Commented by mr W last updated on 12/Oct/21
for unique solution the size of both squares must be given.
$${for}\:{unique}\:{solution}\:{the}\:{size}\:{of}\:{both} \\ $$$${squares}\:{must}\:{be}\:{given}. \\ $$
Commented by ARUNG_Brandon_MBU last updated on 12/Oct/21
OK Sir. But the question is How big is y?
$$\mathrm{OK}\:\mathrm{Sir}.\:\mathrm{But}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\boldsymbol{\mathrm{How}}\:\boldsymbol{\mathrm{big}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{y}}? \\ $$
Commented by mr W last updated on 12/Oct/21
the question is how big can y be. if the second square is the same as the first one, then 1≤y≤1.6006.
$${the}\:{question}\:{is}\:{how}\:{big}\:{can}\:{y}\:{be}. \\ $$$${if}\:{the}\:{second}\:{square}\:{is}\:{the}\:{same}\:{as} \\ $$$${the}\:{first}\:{one},\:{then}\:\mathrm{1}\leqslant{y}\leqslant\mathrm{1}.\mathrm{6006}. \\ $$
Answered by mr W last updated on 12/Oct/21
Commented by mr W last updated on 12/Oct/21
CB=a cos α CD=a sin α x_F =1+a cos α+(√2)acos (45+90−α) x_F =1+a cos α+(√2)a sin (α−45) x_F =1+a cos α+a (sin α−cos α) x_F =1+a sin α y_F =(√2)a sin (45+90−α) y_F =(√2)a cos (α−45) y_F =a (cos α+sin α) ((y−1)/(1+a(cos α+sin α)))=((a(cos α+sin β)−1)/(1+a sin α)) for a=1: y=1+((sin 2α)/(1+sin α)) y_(max) ≈1.6006
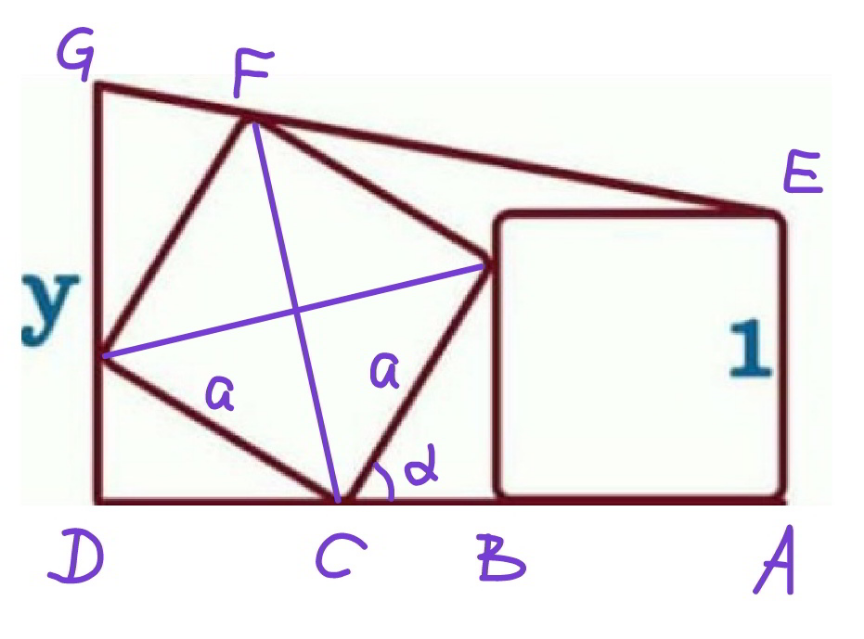
$${CB}={a}\:\mathrm{cos}\:\alpha \\ $$$${CD}={a}\:\mathrm{sin}\:\alpha \\ $$$${x}_{{F}} =\mathrm{1}+{a}\:\mathrm{cos}\:\alpha+\sqrt{\mathrm{2}}{a}\mathrm{cos}\:\left(\mathrm{45}+\mathrm{90}−\alpha\right) \\ $$$${x}_{{F}} =\mathrm{1}+{a}\:\mathrm{cos}\:\alpha+\sqrt{\mathrm{2}}{a}\:\mathrm{sin}\:\left(\alpha−\mathrm{45}\right) \\ $$$${x}_{{F}} =\mathrm{1}+{a}\:\mathrm{cos}\:\alpha+{a}\:\left(\mathrm{sin}\:\alpha−\mathrm{cos}\:\alpha\right) \\ $$$${x}_{{F}} =\mathrm{1}+{a}\:\mathrm{sin}\:\alpha \\ $$$${y}_{{F}} =\sqrt{\mathrm{2}}{a}\:\mathrm{sin}\:\left(\mathrm{45}+\mathrm{90}−\alpha\right) \\ $$$${y}_{{F}} =\sqrt{\mathrm{2}}{a}\:\mathrm{cos}\:\left(\alpha−\mathrm{45}\right) \\ $$$${y}_{{F}} ={a}\:\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right) \\ $$$$\frac{{y}−\mathrm{1}}{\mathrm{1}+{a}\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)}=\frac{{a}\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\beta\right)−\mathrm{1}}{\mathrm{1}+{a}\:\mathrm{sin}\:\alpha} \\ $$$${for}\:{a}=\mathrm{1}: \\ $$$${y}=\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{1}+\mathrm{sin}\:\alpha} \\ $$$${y}_{{max}} \approx\mathrm{1}.\mathrm{6006} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 12/Oct/21
Thank you Sir
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$
Commented by Tawa11 last updated on 12/Oct/21
great sir.
$$\mathrm{great}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *