Question Number 156529 by mnjuly1970 last updated on 12/Oct/21
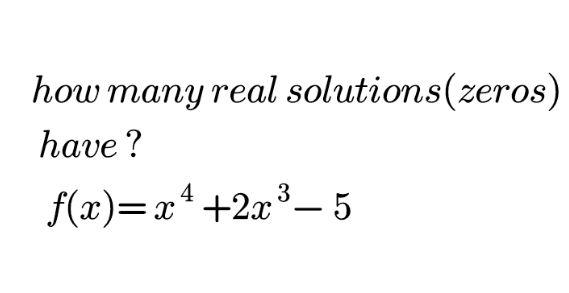
Answered by mr W last updated on 12/Oct/21
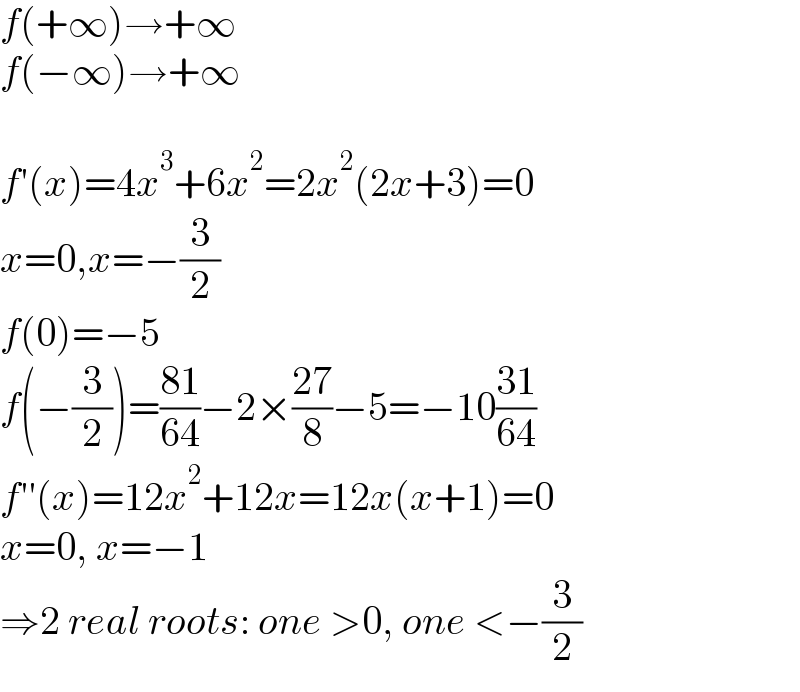
$${f}\left(+\infty\right)\rightarrow+\infty \\ $$$${f}\left(−\infty\right)\rightarrow+\infty \\ $$$$ \\ $$$${f}'\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} =\mathrm{2}{x}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0},{x}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${f}\left(\mathrm{0}\right)=−\mathrm{5} \\ $$$${f}\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{81}}{\mathrm{64}}−\mathrm{2}×\frac{\mathrm{27}}{\mathrm{8}}−\mathrm{5}=−\mathrm{10}\frac{\mathrm{31}}{\mathrm{64}} \\ $$$${f}''\left({x}\right)=\mathrm{12}{x}^{\mathrm{2}} +\mathrm{12}{x}=\mathrm{12}{x}\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0},\:{x}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}\:{real}\:{roots}:\:{one}\:>\mathrm{0},\:{one}\:<−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 12/Oct/21

Commented by mnjuly1970 last updated on 12/Oct/21

$${grateful}\:{sir}\:{W} \\ $$
