Menu Close

Question-156532

Tinku Tara 0 Comments
Pin




Question Number 156532 by MathSh last updated on 12/Oct/21
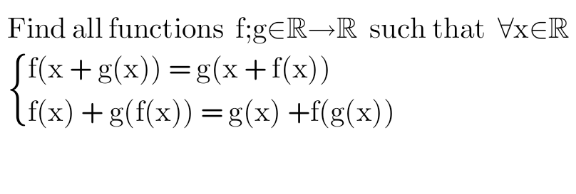
Answered by Rasheed.Sindhi last updated on 13/Oct/21
When f(x),g(x) are constant or linear. { ((f( x+g(x) )=g( x+f(x) ))),((f(x)+g( f(x) )=g(x)+f( g(x) ))) :} Assuming that f(x) and g(x) are both linear: f(x)=ax+b & g(x)=cx+d { ((f( x+cx+d )=g( x+ax+b ))),((ax+b+g( ax+b )=cx+d+f( cx+d ))) :} { ((f( (c+1)x+d )=g( (a+1)x+b ))),((ax+b+g( ax+b )=cx+d+f( cx+d ))) :} { ((a((c+1)x+d)+b=c((a+1)x+b)+d)),((ax+b+c(ax+b)+d=cx+d+a(cx+d)+b)) :} { ((a(c+1)x−c(a+1)x=bc+d−ad−b)),((a(1+c)x+b+bc+d=d+c(a+1)x+ad+b)) :} { (((a−c)x=bc−ad+d−b)),(({a−c}x=ad−bc)) :} ⇒bc−ad+d−b=ad−bc 2bc−b=2ad−d d=((b(2c−1))/(2a−1)) f(x)=ax+b g(x)=cx+((b(2c−1))/(2a−1)) determinant (( determinant ((( determinant (((f(x)=ax+b)),((g(x)=cx+((b(2c−1))/(2a−1));a≠1/2))) ))))) For examples: •a=c=1,b=0 f(x)=x ,g(x)=x a=b=c=1: f(x)=x+1 g(x)=x+1
$$\:\:\:\:\:\mathrm{When}\:\mathrm{f}\left(\mathrm{x}\right),\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{are}\:\boldsymbol{\mathrm{constant}}\:\mathrm{or} \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{linear}}. \\ $$$$\begin{cases}{\mathrm{f}\left(\:\mathrm{x}+\mathrm{g}\left(\mathrm{x}\right)\:\right)=\mathrm{g}\left(\:\mathrm{x}+\mathrm{f}\left(\mathrm{x}\right)\:\right)}\\{\mathrm{f}\left(\mathrm{x}\right)+\mathrm{g}\left(\:\mathrm{f}\left(\mathrm{x}\right)\:\right)=\mathrm{g}\left(\mathrm{x}\right)+\mathrm{f}\left(\:\mathrm{g}\left(\mathrm{x}\right)\:\right)}\end{cases}\:\: \\ $$$$\mathrm{Assuming}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{are}\:\mathrm{both} \\ $$$$\mathrm{linear}:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}+\mathrm{b}\:\&\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{cx}+\mathrm{d} \\ $$$$\begin{cases}{\mathrm{f}\left(\:\mathrm{x}+\mathrm{cx}+\mathrm{d}\:\right)=\mathrm{g}\left(\:\mathrm{x}+\mathrm{ax}+\mathrm{b}\:\right)}\\{\mathrm{ax}+\mathrm{b}+\mathrm{g}\left(\:\mathrm{ax}+\mathrm{b}\:\right)=\mathrm{cx}+\mathrm{d}+\mathrm{f}\left(\:\mathrm{cx}+\mathrm{d}\:\right)}\end{cases}\: \\ $$$$\begin{cases}{\mathrm{f}\left(\:\left(\mathrm{c}+\mathrm{1}\right)\mathrm{x}+\mathrm{d}\:\right)=\mathrm{g}\left(\:\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}+\mathrm{b}\:\right)}\\{\mathrm{ax}+\mathrm{b}+\mathrm{g}\left(\:\mathrm{ax}+\mathrm{b}\:\right)=\mathrm{cx}+\mathrm{d}+\mathrm{f}\left(\:\mathrm{cx}+\mathrm{d}\:\right)}\end{cases}\: \\ $$$$\begin{cases}{\mathrm{a}\left(\left(\mathrm{c}+\mathrm{1}\right)\mathrm{x}+\mathrm{d}\right)+\mathrm{b}=\mathrm{c}\left(\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}+\mathrm{b}\right)+\mathrm{d}}\\{\mathrm{ax}+\mathrm{b}+\mathrm{c}\left(\mathrm{ax}+\mathrm{b}\right)+\mathrm{d}=\mathrm{cx}+\mathrm{d}+\mathrm{a}\left(\mathrm{cx}+\mathrm{d}\right)+\mathrm{b}}\end{cases}\: \\ $$$$\begin{cases}{\mathrm{a}\left(\mathrm{c}+\mathrm{1}\right)\mathrm{x}−\mathrm{c}\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}=\mathrm{bc}+\mathrm{d}−\mathrm{ad}−\mathrm{b}}\\{\mathrm{a}\left(\mathrm{1}+\mathrm{c}\right)\mathrm{x}+\mathrm{b}+\mathrm{bc}+\mathrm{d}=\mathrm{d}+\mathrm{c}\left(\mathrm{a}+\mathrm{1}\right)\mathrm{x}+\mathrm{ad}+\mathrm{b}}\end{cases}\:\:\: \\ $$$$\begin{cases}{\left(\mathrm{a}−\mathrm{c}\right)\mathrm{x}=\mathrm{bc}−\mathrm{ad}+\mathrm{d}−\mathrm{b}}\\{\left\{\mathrm{a}−\mathrm{c}\right\}\mathrm{x}=\mathrm{ad}−\mathrm{bc}}\end{cases}\:\:\: \\ $$$$\Rightarrow\mathrm{bc}−\mathrm{ad}+\mathrm{d}−\mathrm{b}=\mathrm{ad}−\mathrm{bc} \\ $$$$\:\:\:\:\:\mathrm{2bc}−\mathrm{b}=\mathrm{2ad}−\mathrm{d} \\ $$$$\:\:\:\:\mathrm{d}=\frac{\mathrm{b}\left(\mathrm{2c}−\mathrm{1}\right)}{\mathrm{2a}−\mathrm{1}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}+\mathrm{b} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{cx}+\frac{\mathrm{b}\left(\mathrm{2c}−\mathrm{1}\right)}{\mathrm{2a}−\mathrm{1}} \\ $$$$\:\begin{array}{|c|}{\begin{array}{|c|}{\:\begin{array}{|c|c|}{\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}+\mathrm{b}}\\{\mathrm{g}\left(\mathrm{x}\right)=\mathrm{cx}+\frac{\mathrm{b}\left(\mathrm{2c}−\mathrm{1}\right)}{\mathrm{2a}−\mathrm{1}};\mathrm{a}\neq\mathrm{1}/\mathrm{2}}\\\hline\end{array}\:\:}\\\hline\end{array}}\\\hline\end{array}\:\: \\ $$$$\mathrm{For}\:\mathrm{examples}: \\ $$$$\bullet\mathrm{a}=\mathrm{c}=\mathrm{1},\mathrm{b}=\mathrm{0} \\ $$$$\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}\:,\mathrm{g}\left(\mathrm{x}\right)=\mathrm{x} \\ $$$$\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{1}: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}+\mathrm{1} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{x}+\mathrm{1} \\ $$
Commented by MathSh last updated on 13/Oct/21
Perfect dear Ser, thankyou
$$\mathrm{Perfect}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thankyou} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *