Question-156535

Question Number 156535 by MathSh last updated on 12/Oct/21

Answered by Rasheed.Sindhi last updated on 12/Oct/21

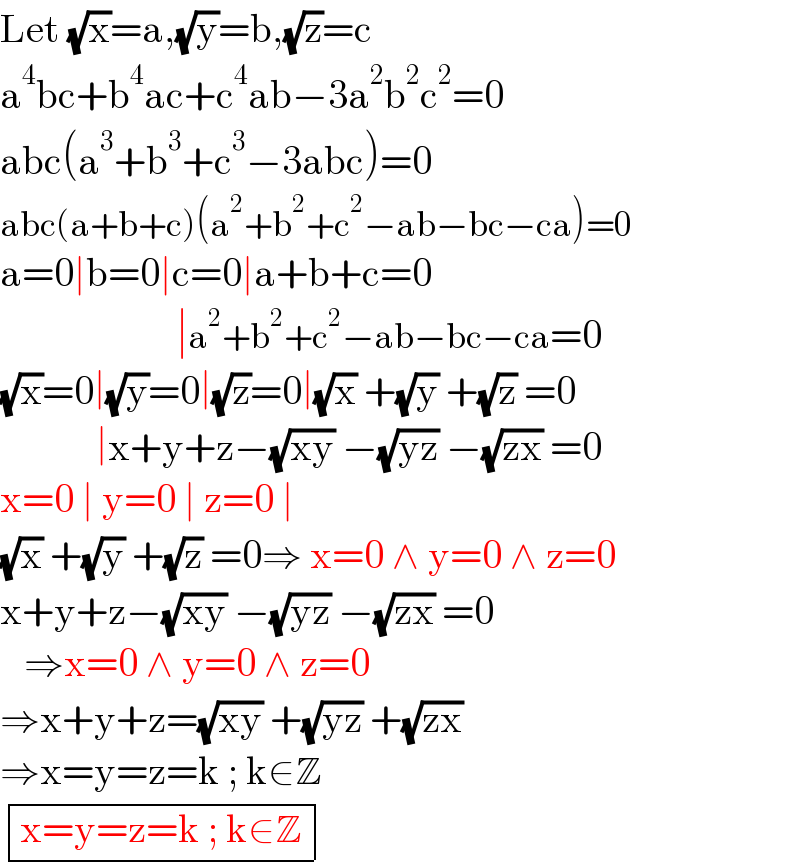
Let (√x)=a,(√y)=b,(√z)=c a^4 bc+b^4 ac+c^4 ab−3a^2 b^2 c^2 =0 abc(a^3 +b^3 +c^3 −3abc)=0 abc(a+b+c)(a^2 +b^2 +c^2 −ab−bc−ca)=0 a=0∣b=0∣c=0∣a+b+c=0 ∣a^2 +b^2 +c^2 −ab−bc−ca=0 (√x)=0∣(√y)=0∣(√z)=0∣(√x) +(√y) +(√z) =0 ∣x+y+z−(√(xy)) −(√(yz)) −(√(zx)) =0 x=0 ∣ y=0 ∣ z=0 ∣ (√x) +(√y) +(√z) =0⇒ x=0 ∧ y=0 ∧ z=0 x+y+z−(√(xy)) −(√(yz)) −(√(zx)) =0 ⇒x=0 ∧ y=0 ∧ z=0 ⇒x+y+z=(√(xy)) +(√(yz)) +(√(zx)) ⇒x=y=z=k ; k∈Z determinant (((x=y=z=k ; k∈Z)))

$$\mathrm{Let}\:\sqrt{\mathrm{x}}=\mathrm{a},\sqrt{\mathrm{y}}=\mathrm{b},\sqrt{\mathrm{z}}=\mathrm{c} \\ $$$$\mathrm{a}^{\mathrm{4}} \mathrm{bc}+\mathrm{b}^{\mathrm{4}} \mathrm{ac}+\mathrm{c}^{\mathrm{4}} \mathrm{ab}−\mathrm{3a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{abc}\left(\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} −\mathrm{3abc}\right)=\mathrm{0} \\ $$$$\mathrm{abc}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{ab}−\mathrm{bc}−\mathrm{ca}\right)=\mathrm{0} \\ $$$$\mathrm{a}=\mathrm{0}\mid\mathrm{b}=\mathrm{0}\mid\mathrm{c}=\mathrm{0}\mid\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{ab}−\mathrm{bc}−\mathrm{ca}=\mathrm{0} \\ $$$$\sqrt{\mathrm{x}}=\mathrm{0}\mid\sqrt{\mathrm{y}}=\mathrm{0}\mid\sqrt{\mathrm{z}}=\mathrm{0}\mid\sqrt{\mathrm{x}}\:+\sqrt{\mathrm{y}}\:+\sqrt{\mathrm{z}}\:=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mid\mathrm{x}+\mathrm{y}+\mathrm{z}−\sqrt{\mathrm{xy}}\:−\sqrt{\mathrm{yz}}\:−\sqrt{\mathrm{zx}}\:=\mathrm{0} \\ $$$$\mathrm{x}=\mathrm{0}\:\mid\:\mathrm{y}=\mathrm{0}\:\mid\:\mathrm{z}=\mathrm{0}\:\mid \\ $$$$\sqrt{\mathrm{x}}\:+\sqrt{\mathrm{y}}\:+\sqrt{\mathrm{z}}\:=\mathrm{0}\Rightarrow\:\mathrm{x}=\mathrm{0}\:\wedge\:\mathrm{y}=\mathrm{0}\:\wedge\:\mathrm{z}=\mathrm{0} \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{z}−\sqrt{\mathrm{xy}}\:−\sqrt{\mathrm{yz}}\:−\sqrt{\mathrm{zx}}\:=\mathrm{0} \\ $$$$\:\:\:\Rightarrow\mathrm{x}=\mathrm{0}\:\wedge\:\mathrm{y}=\mathrm{0}\:\wedge\:\mathrm{z}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}+\mathrm{y}+\mathrm{z}=\sqrt{\mathrm{xy}}\:+\sqrt{\mathrm{yz}}\:+\sqrt{\mathrm{zx}}\: \\ $$$$\Rightarrow\mathrm{x}=\mathrm{y}=\mathrm{z}=\mathrm{k}\:;\:\mathrm{k}\in\mathbb{Z} \\ $$$$\begin{array}{|c|}{\mathrm{x}=\mathrm{y}=\mathrm{z}=\mathrm{k}\:;\:\mathrm{k}\in\mathbb{Z}}\\\hline\end{array} \\ $$

Commented by MathSh last updated on 12/Oct/21

$$\mathrm{Nice}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply