Question-15667

Question Number 15667 by tawa tawa last updated on 12/Jun/17

Commented by mrW1 last updated on 12/Jun/17

diagram is not to understand. please give a clear diagram.

$$\mathrm{diagram}\:\mathrm{is}\:\mathrm{not}\:\mathrm{to}\:\mathrm{understand}.\:\mathrm{please} \\ $$$$\mathrm{give}\:\mathrm{a}\:\mathrm{clear}\:\mathrm{diagram}. \\ $$

Commented by tawa tawa last updated on 12/Jun/17

Answered by mrW1 last updated on 12/Jun/17

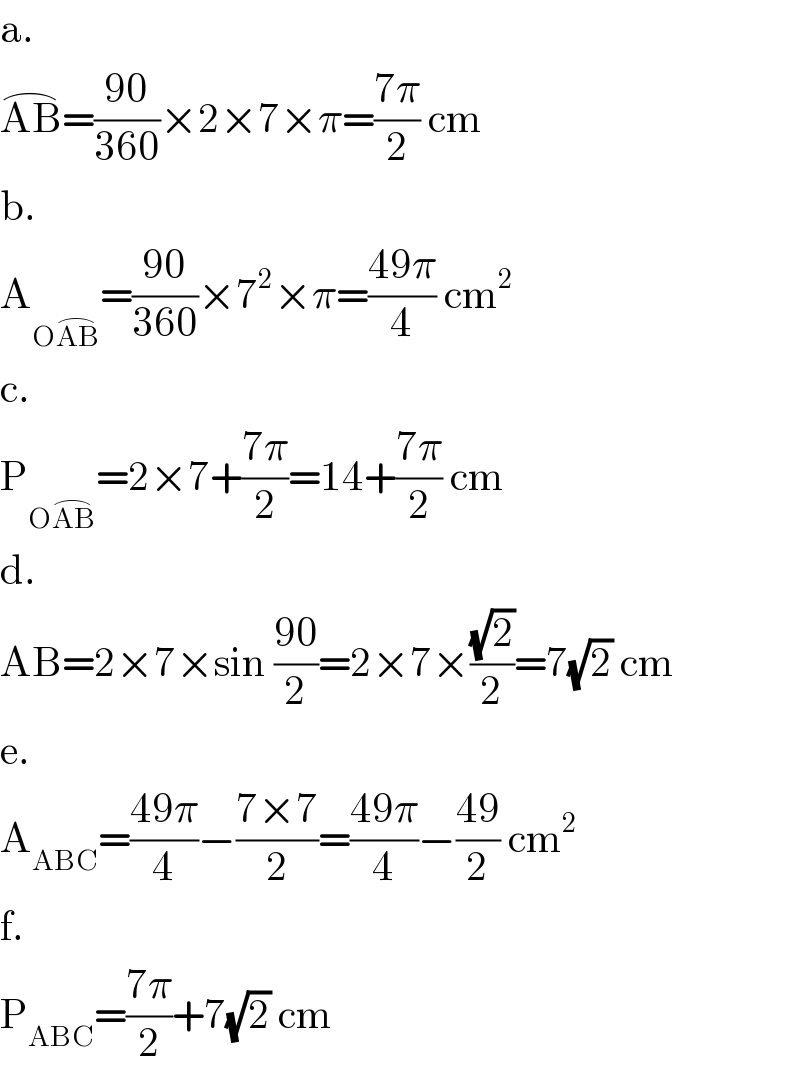
a. AB^(⌢) =((90)/(360))×2×7×π=((7π)/2) cm b. A_(OAB^(⌢) ) =((90)/(360))×7^2 ×π=((49π)/4) cm^2 c. P_(OAB^(⌢) ) =2×7+((7π)/2)=14+((7π)/2) cm d. AB=2×7×sin ((90)/2)=2×7×((√2)/2)=7(√2) cm e. A_(ABC) =((49π)/4)−((7×7)/2)=((49π)/4)−((49)/2) cm^2 f. P_(ABC) =((7π)/2)+7(√2) cm

$$\mathrm{a}. \\ $$$$\overset{\frown} {\mathrm{AB}}=\frac{\mathrm{90}}{\mathrm{360}}×\mathrm{2}×\mathrm{7}×\pi=\frac{\mathrm{7}\pi}{\mathrm{2}}\:\mathrm{cm} \\ $$$$\mathrm{b}. \\ $$$$\mathrm{A}_{\mathrm{O}\overset{\frown} {\mathrm{AB}}} =\frac{\mathrm{90}}{\mathrm{360}}×\mathrm{7}^{\mathrm{2}} ×\pi=\frac{\mathrm{49}\pi}{\mathrm{4}}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$\mathrm{c}. \\ $$$$\mathrm{P}_{\mathrm{O}\overset{\frown} {\mathrm{AB}}} =\mathrm{2}×\mathrm{7}+\frac{\mathrm{7}\pi}{\mathrm{2}}=\mathrm{14}+\frac{\mathrm{7}\pi}{\mathrm{2}}\:\mathrm{cm} \\ $$$$\mathrm{d}. \\ $$$$\mathrm{AB}=\mathrm{2}×\mathrm{7}×\mathrm{sin}\:\frac{\mathrm{90}}{\mathrm{2}}=\mathrm{2}×\mathrm{7}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{7}\sqrt{\mathrm{2}}\:\mathrm{cm} \\ $$$$\mathrm{e}. \\ $$$$\mathrm{A}_{\mathrm{ABC}} =\frac{\mathrm{49}\pi}{\mathrm{4}}−\frac{\mathrm{7}×\mathrm{7}}{\mathrm{2}}=\frac{\mathrm{49}\pi}{\mathrm{4}}−\frac{\mathrm{49}}{\mathrm{2}}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$\mathrm{f}. \\ $$$$\mathrm{P}_{\mathrm{ABC}} =\frac{\mathrm{7}\pi}{\mathrm{2}}+\mathrm{7}\sqrt{\mathrm{2}}\:\mathrm{cm} \\ $$

Commented by mrW1 last updated on 12/Jun/17