Question-156671

Question Number 156671 by cortano last updated on 14/Oct/21

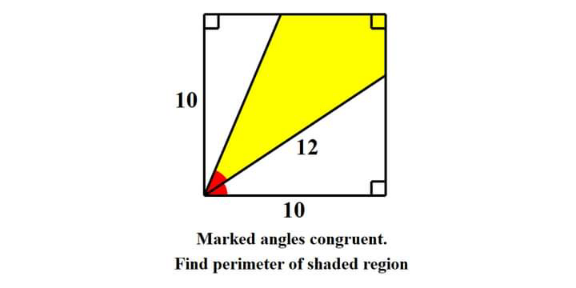
Answered by som(math1967) last updated on 14/Oct/21

Commented by som(math1967) last updated on 14/Oct/21

c o s α = \frac{10}{12} = \frac{5}{6}

s i n α = \frac{\sqrt{11}}{6}

s i n 2 α = 2 \times \frac{\sqrt{11}}{6} \times \frac{5}{6} = \frac{5 \sqrt{11}}{18}

a g a i n s i n 2 α = \frac{L M}{A L}

\frac{10}{A L} = \frac{5 \sqrt{11}}{18} \Rightarrow A L = \frac{36}{\sqrt{11}} = \frac{36 \sqrt{11}}{11}

{D L}^{2} = {(\frac{36 \sqrt{11}}{11})}^{2} - 10^{2}

D L = \frac{14}{\sqrt{11}} = \frac{14 \sqrt{11}}{11}

L C = (10 - \frac{14 \sqrt{11}}{11})

B N = \sqrt{12^{2} - 10^{2}} = 2 \sqrt{11}

C N = 10 - 2 \sqrt{11}

p e r i m e t e r = A L + L C + C N + A N

= \frac{36 \sqrt{11}}{11} + (10 - \frac{14 \sqrt{11}}{11}) + 10 - 2 \sqrt{11} + 12

= 32 + \frac{36 \sqrt{11}}{11} - \frac{36 \sqrt{11}}{11} = 32 u n i t

Commented by cortano last updated on 14/Oct/21

oo yes gave kudos

Commented by otchereabdullai@gmail.com last updated on 14/Oct/21

wow

Commented by Tawa11 last updated on 14/Oct/21

great sir

Answered by john_santu last updated on 15/Oct/21

Commented by cortano last updated on 15/Oct/21

nice

Facebook Tweet Pin