Question Number 156676 by mathlove last updated on 14/Oct/21

Commented by MathSh last updated on 14/Oct/21

$$\frac{\mathrm{2}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}\:+\:\frac{\mathrm{1}}{\mathrm{c}}\:=\:\mathrm{3}\:\Rightarrow\:\frac{\mathrm{21}}{\mathrm{3}}\:=\:\mathrm{7} \\ $$
Answered by som(math1967) last updated on 14/Oct/21

$$\mathrm{60}=\mathrm{27}^{{a}} \Rightarrow\mathrm{60}^{\frac{\mathrm{1}}{{a}}} =\mathrm{27} \\ $$$$\mathrm{60}^{\frac{\mathrm{1}}{{b}}} =\mathrm{64}\:\:\:\:,\mathrm{60}^{\frac{\mathrm{1}}{{c}}} =\mathrm{125} \\ $$$$\mathrm{60}^{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}} =\mathrm{3}^{\mathrm{3}} ×\mathrm{4}^{\mathrm{3}} ×\mathrm{5}^{\mathrm{3}} \\ $$$$\left(\mathrm{60}\right)^{\frac{{ab}+{bc}+{ca}}{{abc}}} =\left(\mathrm{60}\right)^{\mathrm{3}} \\ $$$$\:\frac{{ab}+{bc}+{ca}}{{abc}}=\mathrm{3} \\ $$$$\frac{{abc}}{{ab}+{bc}+{ca}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\therefore\frac{\mathrm{21}\boldsymbol{{abc}}}{\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ca}}}=\mathrm{21}×\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{7}\:\boldsymbol{{ans}} \\ $$
Answered by Rasheed.Sindhi last updated on 14/Oct/21

$$\:\:\:\:\:\:\:\:\:\:\mathbb{A}\mathrm{n}\:\mathbb{A}\mathrm{lternate}\:\mathbb{A}\mathrm{pproach} \\ $$$$\left(\mathrm{3}^{{a}} \right)^{\mathrm{3}} =\left(\mathrm{4}^{{b}} \right)^{\mathrm{3}} =\left(\mathrm{5}^{{c}} \right)^{\mathrm{3}} =\mathrm{60} \\ $$$$\left(\mathrm{3}^{{a}} \right)^{\mathrm{3}} \left(\mathrm{4}^{{b}} \right)^{\mathrm{3}} \left(\mathrm{5}^{{c}} \right)^{\mathrm{3}} =\left(\mathrm{60}\right)^{\mathrm{3}} \\ $$$$\mathrm{3}^{{a}} \mathrm{4}^{{b}} \mathrm{5}^{{c}} =\mathrm{60}=\mathrm{3}^{\mathrm{1}} .\mathrm{4}^{\mathrm{1}} .\mathrm{5}^{\mathrm{1}} \\ $$$${a}={b}={c}=\mathrm{1} \\ $$$$\frac{\mathrm{21}{abc}}{{ab}+{bc}+{ca}}=\frac{\mathrm{21}.\mathrm{1}.\mathrm{1}.\mathrm{1}}{\mathrm{1}.\mathrm{1}+\mathrm{1}.\mathrm{1}+\mathrm{1}.\mathrm{1}}=\frac{\mathrm{21}}{\mathrm{3}}=\mathrm{7} \\ $$$$ \\ $$
Commented by mr W last updated on 14/Oct/21

$${but}\:{a}={b}={c}=\mathrm{1}\:{doesn}'{t}\:{fulfill}\:{the} \\ $$$${given}\:{condition}. \\ $$
Commented by Rasheed.Sindhi last updated on 14/Oct/21
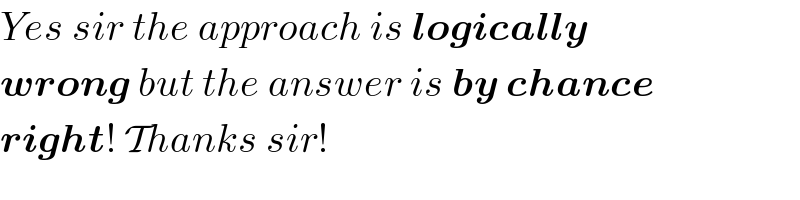
$${Yes}\:{sir}\:{the}\:{approach}\:{is}\:\boldsymbol{{logically}} \\ $$$$\boldsymbol{{wrong}}\:{but}\:{the}\:{answer}\:{is}\:\boldsymbol{{by}}\:\boldsymbol{{chance}} \\ $$$$\boldsymbol{{right}}!\:\mathcal{T}{hanks}\:{sir}! \\ $$
Answered by john_santu last updated on 14/Oct/21
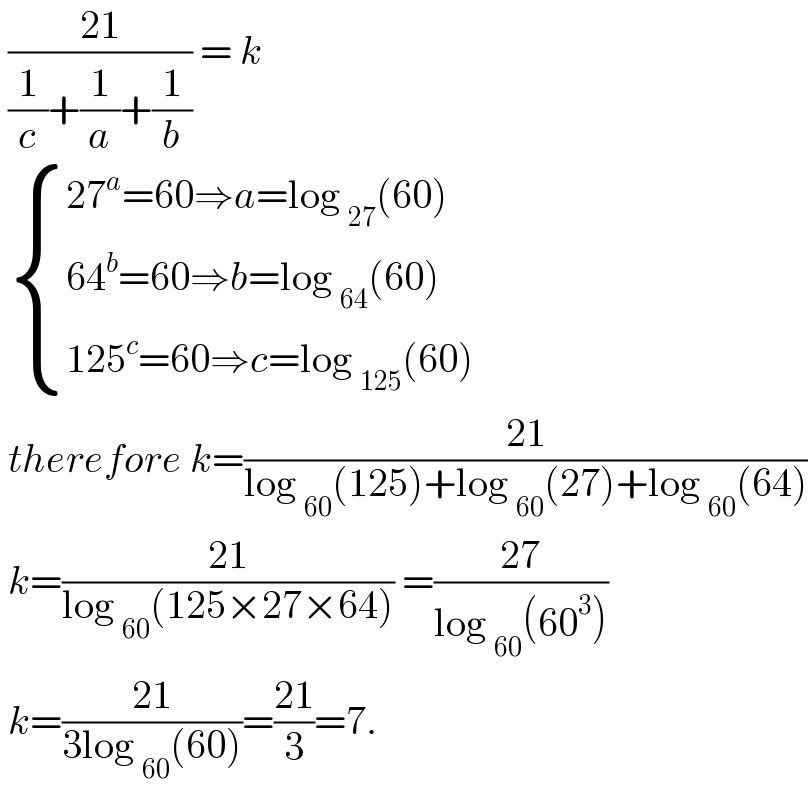
$$\:\frac{\mathrm{21}}{\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}}\:=\:{k} \\ $$$$\:\begin{cases}{\mathrm{27}^{{a}} =\mathrm{60}\Rightarrow{a}=\mathrm{log}\:_{\mathrm{27}} \left(\mathrm{60}\right)}\\{\mathrm{64}^{{b}} =\mathrm{60}\Rightarrow{b}=\mathrm{log}\:_{\mathrm{64}} \left(\mathrm{60}\right)}\\{\mathrm{125}^{{c}} =\mathrm{60}\Rightarrow{c}=\mathrm{log}\:_{\mathrm{125}} \left(\mathrm{60}\right)}\end{cases} \\ $$$$\:{therefore}\:{k}=\frac{\mathrm{21}}{\mathrm{log}\:_{\mathrm{60}} \left(\mathrm{125}\right)+\mathrm{log}\:_{\mathrm{60}} \left(\mathrm{27}\right)+\mathrm{log}\:_{\mathrm{60}} \left(\mathrm{64}\right)} \\ $$$$\:{k}=\frac{\mathrm{21}}{\mathrm{log}\:_{\mathrm{60}} \left(\mathrm{125}×\mathrm{27}×\mathrm{64}\right)}\:=\frac{\mathrm{27}}{\mathrm{log}\:_{\mathrm{60}} \left(\mathrm{60}^{\mathrm{3}} \right)} \\ $$$$\:{k}=\frac{\mathrm{21}}{\mathrm{3log}\:_{\mathrm{60}} \left(\mathrm{60}\right)}=\frac{\mathrm{21}}{\mathrm{3}}=\mathrm{7}.\: \\ $$
Commented by cortano last updated on 14/Oct/21

$$\mathrm{waw} \\ $$$$ \\ $$
Commented by peter frank last updated on 14/Oct/21

$$\mathrm{great} \\ $$
