Question-156841

Question Number 156841 by mnjuly1970 last updated on 16/Oct/21

Answered by gsk2684 last updated on 16/Oct/21

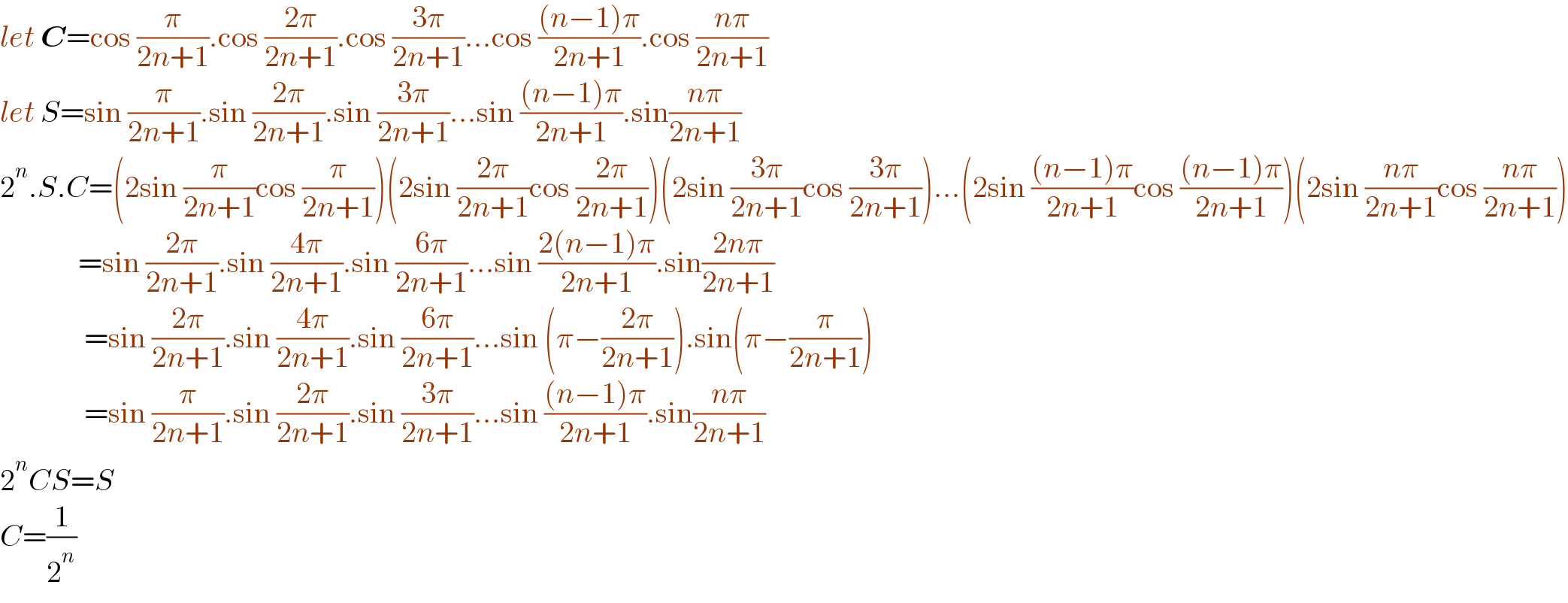
let C=cos (π/(2n+1)).cos ((2π)/(2n+1)).cos ((3π)/(2n+1))...cos (((n−1)π)/(2n+1)).cos ((nπ)/(2n+1)) let S=sin (π/(2n+1)).sin ((2π)/(2n+1)).sin ((3π)/(2n+1))...sin (((n−1)π)/(2n+1)).sin((nπ)/(2n+1)) 2^n .S.C=(2sin (π/(2n+1))cos (π/(2n+1)))(2sin ((2π)/(2n+1))cos ((2π)/(2n+1)))(2sin ((3π)/(2n+1))cos ((3π)/(2n+1)))...(2sin (((n−1)π)/(2n+1))cos (((n−1)π)/(2n+1)))(2sin ((nπ)/(2n+1))cos ((nπ)/(2n+1))) =sin ((2π)/(2n+1)).sin ((4π)/(2n+1)).sin ((6π)/(2n+1))...sin ((2(n−1)π)/(2n+1)).sin((2nπ)/(2n+1)) =sin ((2π)/(2n+1)).sin ((4π)/(2n+1)).sin ((6π)/(2n+1))...sin (π−((2π)/(2n+1))).sin(π−(π/(2n+1))) =sin (π/(2n+1)).sin ((2π)/(2n+1)).sin ((3π)/(2n+1))...sin (((n−1)π)/(2n+1)).sin((nπ)/(2n+1)) 2^n CS=S C=(1/2^n )

$${let}\:\boldsymbol{{C}}=\mathrm{cos}\:\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{2}{n}+\mathrm{1}}…\mathrm{cos}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{cos}\:\frac{{n}\pi}{\mathrm{2}{n}+\mathrm{1}} \\ $$$${let}\:{S}=\mathrm{sin}\:\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}{n}+\mathrm{1}}…\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\frac{{n}\pi}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\mathrm{2}^{{n}} .{S}.{C}=\left(\mathrm{2sin}\:\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}\mathrm{cos}\:\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\left(\mathrm{2sin}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\left(\mathrm{2sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}{n}+\mathrm{1}}\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)…\left(\mathrm{2sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}+\mathrm{1}}\mathrm{cos}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\left(\mathrm{2sin}\:\frac{{n}\pi}{\mathrm{2}{n}+\mathrm{1}}\mathrm{cos}\:\frac{{n}\pi}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\:\frac{\mathrm{4}\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\:\frac{\mathrm{6}\pi}{\mathrm{2}{n}+\mathrm{1}}…\mathrm{sin}\:\frac{\mathrm{2}\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\frac{\mathrm{2}{n}\pi}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\:\frac{\mathrm{4}\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\:\frac{\mathrm{6}\pi}{\mathrm{2}{n}+\mathrm{1}}…\mathrm{sin}\:\left(\pi−\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}\right).\mathrm{sin}\left(\pi−\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{sin}\:\frac{\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}{n}+\mathrm{1}}…\mathrm{sin}\:\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}+\mathrm{1}}.\mathrm{sin}\frac{{n}\pi}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\mathrm{2}^{{n}} {CS}={S} \\ $$$${C}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$

Commented by mnjuly1970 last updated on 16/Oct/21

$$\:{very}\:{nice}\:{sir}..{grateful}… \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply