Question Number 156891 by cortano last updated on 16/Oct/21
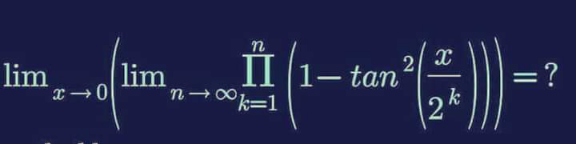
Answered by mindispower last updated on 17/Oct/21
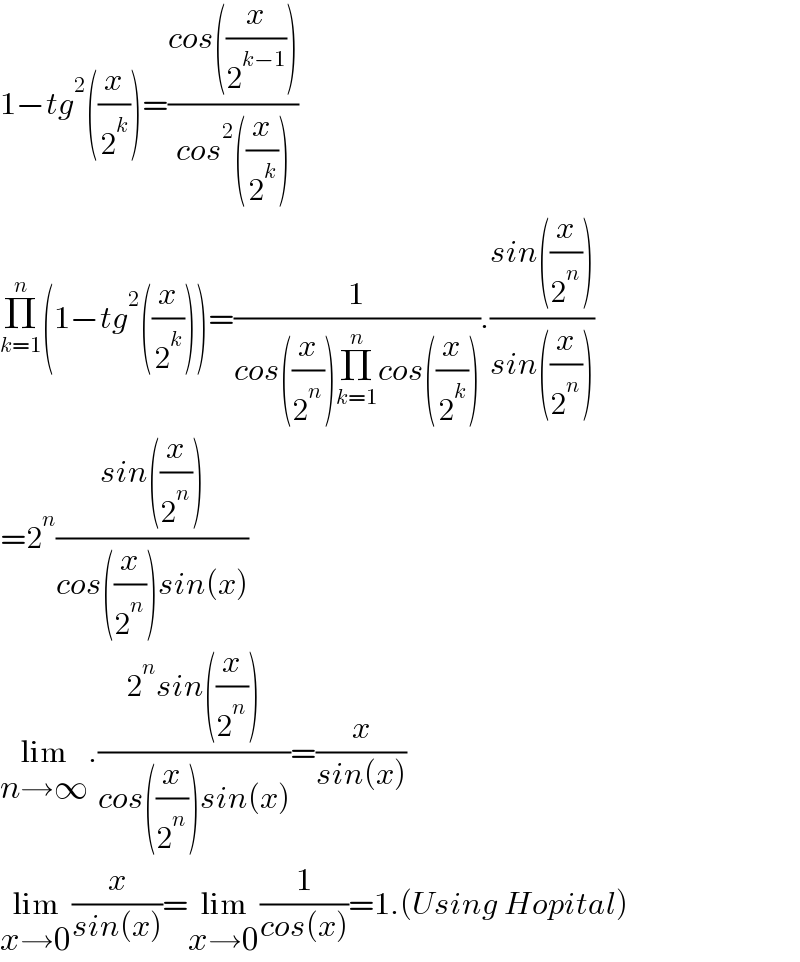
$$\mathrm{1}−{tg}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}^{{k}} }\right)=\frac{{cos}\left(\frac{{x}}{\mathrm{2}^{{k}−\mathrm{1}} }\right)}{{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}^{{k}} }\right)} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}−{tg}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}^{{k}} }\right)\right)=\frac{\mathrm{1}}{{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{cos}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)}.\frac{{sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)}{{sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)} \\ $$$$=\mathrm{2}^{{n}} \frac{{sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)}{{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right){sin}\left({x}\right)} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}.\frac{\mathrm{2}^{{n}} {sin}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)}{{cos}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right){sin}\left({x}\right)}=\frac{{x}}{{sin}\left({x}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}}{{sin}\left({x}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{cos}\left({x}\right)}=\mathrm{1}.\left({Using}\:{Hopital}\right) \\ $$
