Question-156915

Question Number 156915 by mnjuly1970 last updated on 17/Oct/21

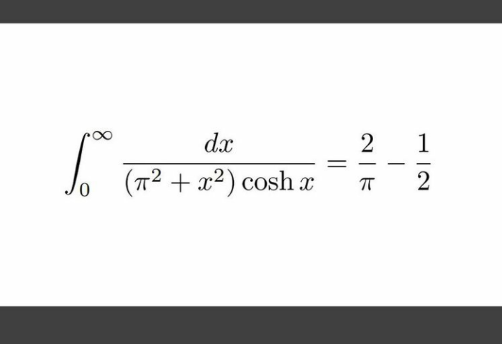
Answered by qaz last updated on 07/Nov/21

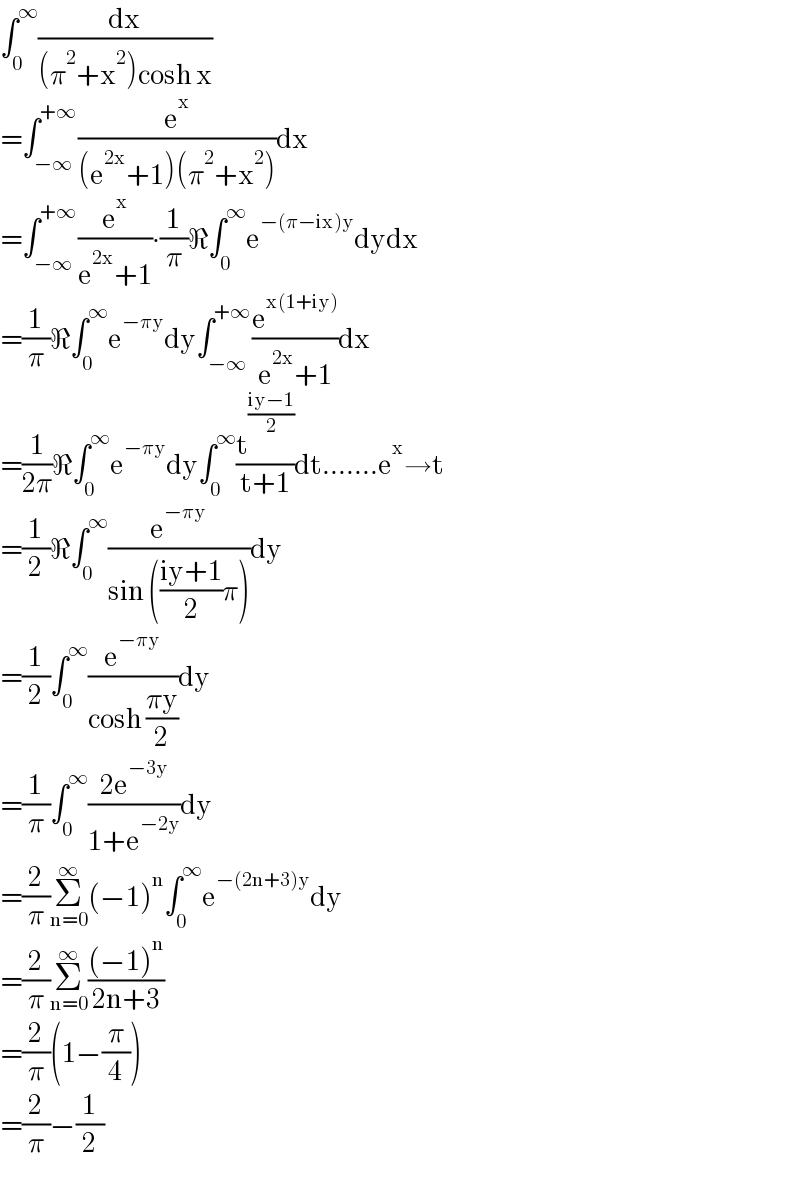
∫_0 ^∞ (dx/((π^2 +x^2 )cosh x)) =∫_(−∞) ^(+∞) (e^x /((e^(2x) +1)(π^2 +x^2 )))dx =∫_(−∞) ^(+∞) (e^x /(e^(2x) +1))∙(1/π)ℜ∫_0 ^∞ e^(−(π−ix)y) dydx =(1/π)ℜ∫_0 ^∞ e^(−πy) dy∫_(−∞) ^(+∞) (e^(x(1+iy)) /(e^(2x) +1))dx =(1/(2π))ℜ∫_0 ^∞ e^(−πy) dy∫_0 ^∞ (t^((iy−1)/2) /(t+1))dt.......e^x →t =(1/2)ℜ∫_0 ^∞ (e^(−πy) /(sin (((iy+1)/2)π)))dy =(1/2)∫_0 ^∞ (e^(−πy) /(cosh ((πy)/2)))dy =(1/π)∫_0 ^∞ ((2e^(−3y) )/(1+e^(−2y) ))dy =(2/π)Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2n+3)y) dy =(2/π)Σ_(n=0) ^∞ (((−1)^n )/(2n+3)) =(2/π)(1−(π/4)) =(2/π)−(1/2)

$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\left(\pi^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)\mathrm{cosh}\:\mathrm{x}} \\ $$$$=\int_{−\infty} ^{+\infty} \frac{\mathrm{e}^{\mathrm{x}} }{\left(\mathrm{e}^{\mathrm{2x}} +\mathrm{1}\right)\left(\pi^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{2x}} +\mathrm{1}}\centerdot\frac{\mathrm{1}}{\pi}\Re\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\pi−\mathrm{ix}\right)\mathrm{y}} \mathrm{dydx} \\ $$$$=\frac{\mathrm{1}}{\pi}\Re\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\pi\mathrm{y}} \mathrm{dy}\int_{−\infty} ^{+\infty} \frac{\mathrm{e}^{\mathrm{x}\left(\mathrm{1}+\mathrm{iy}\right)} }{\mathrm{e}^{\mathrm{2x}} +\mathrm{1}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\Re\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\pi\mathrm{y}} \mathrm{dy}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\frac{\mathrm{iy}−\mathrm{1}}{\mathrm{2}}} }{\mathrm{t}+\mathrm{1}}\mathrm{dt}…….\mathrm{e}^{\mathrm{x}} \rightarrow\mathrm{t} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Re\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\pi\mathrm{y}} }{\mathrm{sin}\:\left(\frac{\mathrm{iy}+\mathrm{1}}{\mathrm{2}}\pi\right)}\mathrm{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\pi\mathrm{y}} }{\mathrm{cosh}\:\frac{\pi\mathrm{y}}{\mathrm{2}}}\mathrm{dy} \\ $$$$=\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2e}^{−\mathrm{3y}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2y}} }\mathrm{dy} \\ $$$$=\frac{\mathrm{2}}{\pi}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{2n}+\mathrm{3}\right)\mathrm{y}} \mathrm{dy} \\ $$$$=\frac{\mathrm{2}}{\pi}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{3}} \\ $$$$=\frac{\mathrm{2}}{\pi}\left(\mathrm{1}−\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\frac{\mathrm{2}}{\pi}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply