Menu Close

Question-156966

Tinku Tara 0 Comments
Pin




Question Number 156966 by Armindo last updated on 17/Oct/21
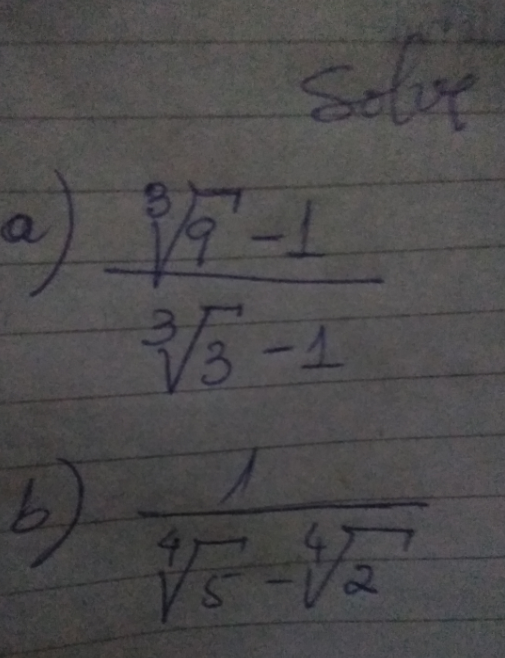
Commented by Armindo last updated on 17/Oct/21
Helô, I need help...
Answered by Rasheed.Sindhi last updated on 18/Oct/21
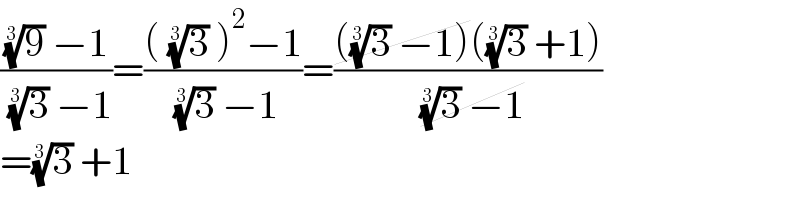
(((9)^(1/3) −1)/( (3)^(1/3) −1))=((( (3)^(1/3) )^2 −1)/( (3)^(1/3) −1))=((((3)^(1/3) −1)((3)^(1/3) +1))/( (3)^(1/3) −1)) =(3)^(1/3) +1
$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}}\:−\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}\:−\mathrm{1}}=\frac{\left(\:\sqrt[{\mathrm{3}}]{\mathrm{3}}\:\right)^{\mathrm{2}} −\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}\:−\mathrm{1}}=\frac{\cancel{\left(\sqrt[{\mathrm{3}}]{\mathrm{3}}\:−\mathrm{1}\right)}\left(\sqrt[{\mathrm{3}}]{\mathrm{3}}\:+\mathrm{1}\right)}{\:\cancel{\sqrt[{\mathrm{3}}]{\mathrm{3}}\:−\mathrm{1}}} \\ $$$$=\sqrt[{\mathrm{3}}]{\mathrm{3}}\:+\mathrm{1} \\ $$
Answered by depressiveshrek last updated on 18/Oct/21
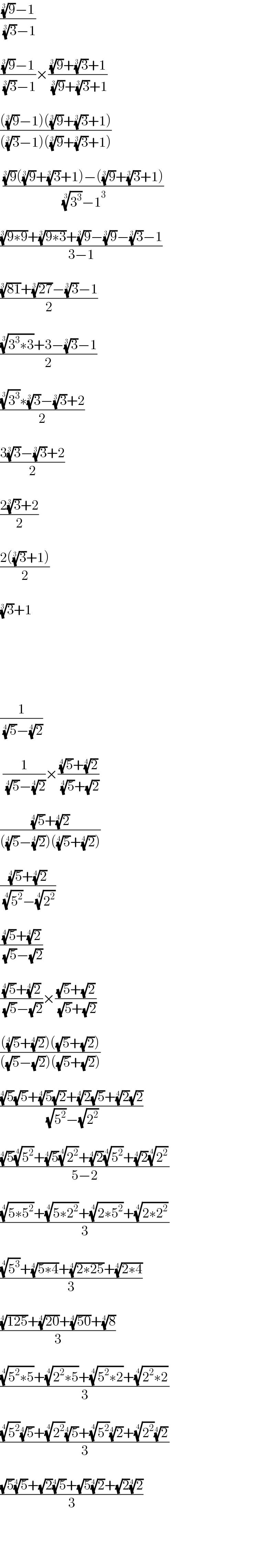
(((9)^(1/3) −1)/( (3)^(1/3) −1)) (((9)^(1/3) −1)/( (3)^(1/3) −1))×(((9)^(1/3) +(3)^(1/3) +1)/( (9)^(1/3) +(3)^(1/3) +1)) ((((9)^(1/3) −1)((9)^(1/3) +(3)^(1/3) +1))/(((3)^(1/3) −1)((9)^(1/3) +(3)^(1/3) +1))) (((9)^(1/3) ((9)^(1/3) +(3)^(1/3) +1)−((9)^(1/3) +(3)^(1/3) +1))/( (3^3 )^(1/3) −1^3 )) ((((9∗9))^(1/3) +((9∗3))^(1/3) +(9)^(1/3) −(9)^(1/3) −(3)^(1/3) −1)/(3−1)) ((((81))^(1/3) +((27))^(1/3) −(3)^(1/3) −1)/2) ((((3^3 ∗3))^(1/3) +3−(3)^(1/3) −1)/2) (((3^3 )^(1/3) ∗(3)^(1/3) −(3)^(1/3) +2)/2) ((3(3)^(1/3) −(3)^(1/3) +2)/2) ((2(3)^(1/3) +2)/2) ((2((3)^(1/3) +1))/2) (3)^(1/3) +1 (1/( (5)^(1/4) −(2)^(1/4) )) (1/( (5)^(1/4) −(2)^(1/4) ))×(((5)^(1/4) +(2)^(1/4) )/( (5)^(1/4) +(√2))) (((5)^(1/4) +(2)^(1/4) )/(((5)^(1/4) −(2)^(1/4) )((5)^(1/4) +(2)^(1/4) ))) (((5)^(1/4) +(2)^(1/4) )/( (5^2 )^(1/4) −(2^2 )^(1/4) )) (((5)^(1/4) +(2)^(1/4) )/( (√5)−(√2))) (((5)^(1/4) +(2)^(1/4) )/( (√5)−(√2)))×(((√5)+(√2))/( (√5)+(√2))) ((((5)^(1/4) +(2)^(1/4) )((√5)+(√2)))/(((√5)−(√2))((√5)+(√2)))) (((5)^(1/4) (√5)+(5)^(1/4) (√2)+(2)^(1/4) (√5)+(2)^(1/4) (√2))/( (√5^2 )−(√2^2 ))) (((5)^(1/4) (5^2 )^(1/4) +(5)^(1/4) (2^2 )^(1/4) +(2)^(1/4) (5^2 )^(1/4) +(2)^(1/4) (2^2 )^(1/4) )/(5−2)) ((((5∗5^2 ))^(1/4) +((5∗2^2 ))^(1/4) +((2∗5^2 ))^(1/4) +((2∗2^2 ))^(1/4) )/3) (((5^3 )^(1/4) +((5∗4))^(1/4) +((2∗25))^(1/4) +((2∗4))^(1/4) )/3) ((((125))^(1/4) +((20))^(1/4) +((50))^(1/4) +(8)^(1/4) )/3) ((((5^2 ∗5))^(1/4) +((2^2 ∗5))^(1/4) +((5^2 ∗2))^(1/4) +((2^2 ∗2))^(1/4) )/3) (((5^2 )^(1/4) (5)^(1/4) +(2^2 )^(1/4) (5)^(1/4) +(5^2 )^(1/4) (2)^(1/4) +(2^2 )^(1/4) (2)^(1/4) )/3) (((√5)(5)^(1/4) +(√2)(5)^(1/4) +(√5)(2)^(1/4) +(√2)(2)^(1/4) )/3)
$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}}−\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}−\mathrm{1}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}}−\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}}−\mathrm{1}}×\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}}+\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{9}}+\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{1}} \\ $$$$\: \\ $$$$\frac{\left(\sqrt[{\mathrm{3}}]{\mathrm{9}}−\mathrm{1}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{9}}+\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{1}\right)}{\left(\sqrt[{\mathrm{3}}]{\mathrm{3}}−\mathrm{1}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{9}}+\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{1}\right)} \\ $$$$\: \\ $$$$\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}}\left(\sqrt[{\mathrm{3}}]{\mathrm{9}}+\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{1}\right)−\left(\sqrt[{\mathrm{3}}]{\mathrm{9}}+\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{1}\right)}{\:\sqrt[{\mathrm{3}}]{\mathrm{3}^{\mathrm{3}} }−\mathrm{1}^{\mathrm{3}} } \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{9}\ast\mathrm{9}}+\sqrt[{\mathrm{3}}]{\mathrm{9}\ast\mathrm{3}}+\sqrt[{\mathrm{3}}]{\mathrm{9}}−\sqrt[{\mathrm{3}}]{\mathrm{9}}−\sqrt[{\mathrm{3}}]{\mathrm{3}}−\mathrm{1}}{\mathrm{3}−\mathrm{1}} \\ $$$$\:\: \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{81}}+\sqrt[{\mathrm{3}}]{\mathrm{27}}−\sqrt[{\mathrm{3}}]{\mathrm{3}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\:\: \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}^{\mathrm{3}} \ast\mathrm{3}}+\mathrm{3}−\sqrt[{\mathrm{3}}]{\mathrm{3}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{3}^{\mathrm{3}} }\ast\sqrt[{\mathrm{3}}]{\mathrm{3}}−\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{2}}{\mathrm{2}} \\ $$$$\: \\ $$$$\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{3}}−\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{2}}{\mathrm{2}} \\ $$$$\: \\ $$$$\frac{\mathrm{2}\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{2}}{\mathrm{2}} \\ $$$$\: \\ $$$$\frac{\mathrm{2}\left(\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\: \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{3}}+\mathrm{1} \\ $$$$\:\: \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{5}}−\sqrt[{\mathrm{4}}]{\mathrm{2}}} \\ $$$$\: \\ $$$$\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{5}}−\sqrt[{\mathrm{4}}]{\mathrm{2}}}×\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}}{\:\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt{\mathrm{2}}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}}{\left(\sqrt[{\mathrm{4}}]{\mathrm{5}}−\sqrt[{\mathrm{4}}]{\mathrm{2}}\right)\left(\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}\right)} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}}{\:\sqrt[{\mathrm{4}}]{\mathrm{5}^{\mathrm{2}} }−\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{2}} }} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}}{\:\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}}{\:\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}}×\frac{\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}} \\ $$$$\: \\ $$$$\frac{\left(\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}\right)\left(\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}\right)}{\left(\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}\right)\left(\sqrt{\mathrm{5}}+\sqrt{\mathrm{2}}\right)} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}}\sqrt{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{5}}\sqrt{\mathrm{2}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}\sqrt{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{5}^{\mathrm{2}} }−\sqrt{\mathrm{2}^{\mathrm{2}} }} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}}\sqrt[{\mathrm{4}}]{\mathrm{5}^{\mathrm{2}} }+\sqrt[{\mathrm{4}}]{\mathrm{5}}\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{2}} }+\sqrt[{\mathrm{4}}]{\mathrm{2}}\sqrt[{\mathrm{4}}]{\mathrm{5}^{\mathrm{2}} }+\sqrt[{\mathrm{4}}]{\mathrm{2}}\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{2}} }}{\mathrm{5}−\mathrm{2}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}\ast\mathrm{5}^{\mathrm{2}} }+\sqrt[{\mathrm{4}}]{\mathrm{5}\ast\mathrm{2}^{\mathrm{2}} }+\sqrt[{\mathrm{4}}]{\mathrm{2}\ast\mathrm{5}^{\mathrm{2}} }+\sqrt[{\mathrm{4}}]{\mathrm{2}\ast\mathrm{2}^{\mathrm{2}} }}{\mathrm{3}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}^{\mathrm{3}} }+\sqrt[{\mathrm{4}}]{\mathrm{5}\ast\mathrm{4}}+\sqrt[{\mathrm{4}}]{\mathrm{2}\ast\mathrm{25}}+\sqrt[{\mathrm{4}}]{\mathrm{2}\ast\mathrm{4}}}{\mathrm{3}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{125}}+\sqrt[{\mathrm{4}}]{\mathrm{20}}+\sqrt[{\mathrm{4}}]{\mathrm{50}}+\sqrt[{\mathrm{4}}]{\mathrm{8}}}{\mathrm{3}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}^{\mathrm{2}} \ast\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{2}} \ast\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{5}^{\mathrm{2}} \ast\mathrm{2}}+\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{2}} \ast\mathrm{2}}}{\mathrm{3}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{5}^{\mathrm{2}} }\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{2}} }\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt[{\mathrm{4}}]{\mathrm{5}^{\mathrm{2}} }\sqrt[{\mathrm{4}}]{\mathrm{2}}+\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{2}} }\sqrt[{\mathrm{4}}]{\mathrm{2}}}{\mathrm{3}} \\ $$$$\: \\ $$$$\frac{\sqrt{\mathrm{5}}\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt{\mathrm{2}}\sqrt[{\mathrm{4}}]{\mathrm{5}}+\sqrt{\mathrm{5}}\sqrt[{\mathrm{4}}]{\mathrm{2}}+\sqrt{\mathrm{2}}\sqrt[{\mathrm{4}}]{\mathrm{2}}}{\mathrm{3}} \\ $$$$\: \\ $$
Commented by Armindo last updated on 18/Oct/21
thanks...I will check the procedure! do you have a book, when I find that solve or This procedure?

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *