Question Number 157035 by Armindo last updated on 18/Oct/21

Commented by Armindo last updated on 18/Oct/21

$${help}… \\ $$
Commented by MJS_new last updated on 18/Oct/21
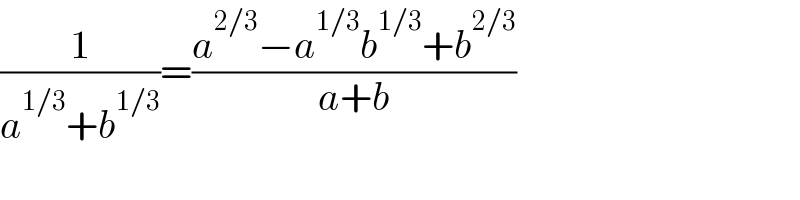
$$\frac{\mathrm{1}}{{a}^{\mathrm{1}/\mathrm{3}} +{b}^{\mathrm{1}/\mathrm{3}} }=\frac{{a}^{\mathrm{2}/\mathrm{3}} −{a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} +{b}^{\mathrm{2}/\mathrm{3}} }{{a}+{b}} \\ $$
Commented by cortano last updated on 19/Oct/21
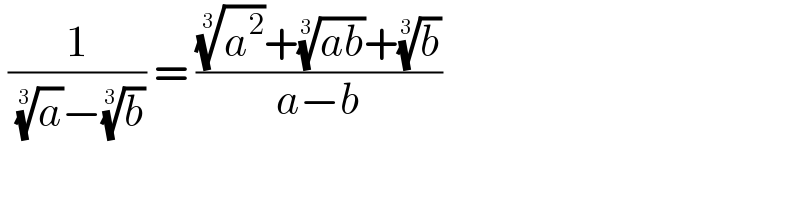
$$\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{a}}−\sqrt[{\mathrm{3}}]{{b}}}\:=\:\frac{\sqrt[{\mathrm{3}}]{{a}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{{ab}}+\sqrt[{\mathrm{3}}]{{b}}}{{a}−{b}} \\ $$
Commented by MJS_new last updated on 19/Oct/21
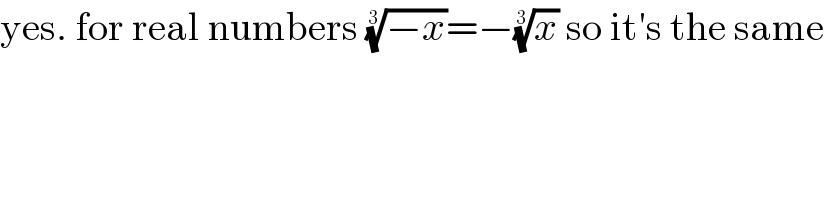
$$\mathrm{yes}.\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}\:\sqrt[{\mathrm{3}}]{−{x}}=−\sqrt[{\mathrm{3}}]{{x}}\:\mathrm{so}\:\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{same} \\ $$
Answered by depressiveshrek last updated on 18/Oct/21
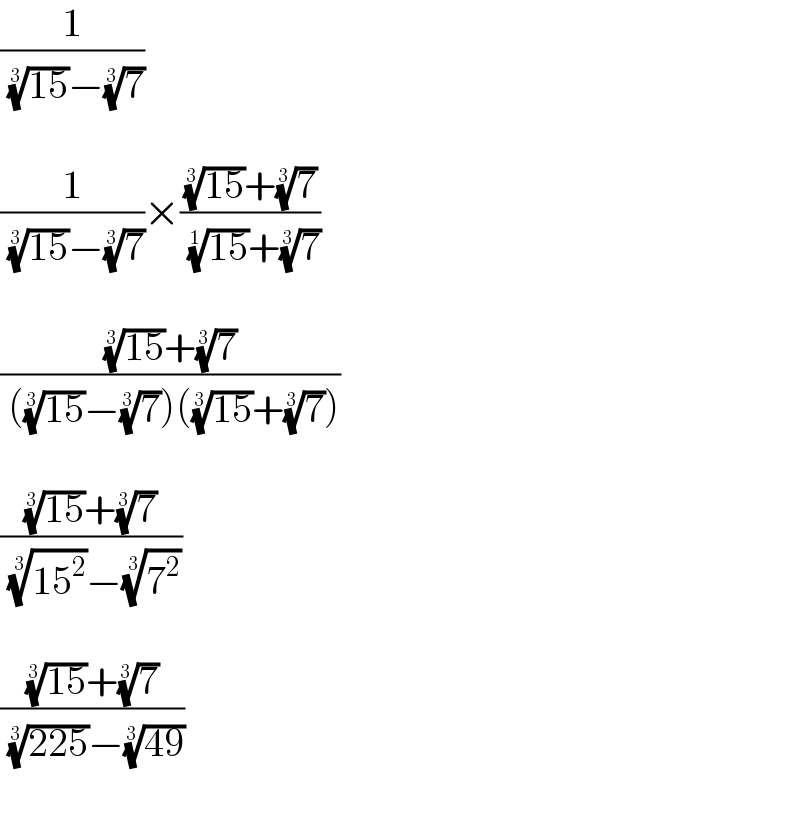
$$\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{15}}−\sqrt[{\mathrm{3}}]{\mathrm{7}}} \\ $$$$\: \\ $$$$\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{15}}−\sqrt[{\mathrm{3}}]{\mathrm{7}}}×\frac{\sqrt[{\mathrm{3}}]{\mathrm{15}}+\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\:\sqrt[{\mathrm{1}}]{\mathrm{15}}+\sqrt[{\mathrm{3}}]{\mathrm{7}}} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{15}}+\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\:\left(\sqrt[{\mathrm{3}}]{\mathrm{15}}−\sqrt[{\mathrm{3}}]{\mathrm{7}}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{15}}+\sqrt[{\mathrm{3}}]{\mathrm{7}}\right)} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{15}}+\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{15}^{\mathrm{2}} }−\sqrt[{\mathrm{3}}]{\mathrm{7}^{\mathrm{2}} }} \\ $$$$\: \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{15}}+\sqrt[{\mathrm{3}}]{\mathrm{7}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{225}}−\sqrt[{\mathrm{3}}]{\mathrm{49}}} \\ $$$$\: \\ $$
Commented by MJS_new last updated on 18/Oct/21
$$\mathrm{you}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{any}\:\mathrm{better}?! \\ $$
