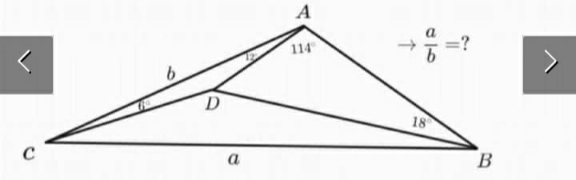
Question Number 157045 by MathSh last updated on 18/Oct/21
Commented by Tawa11 last updated on 19/Oct/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 19/Oct/21
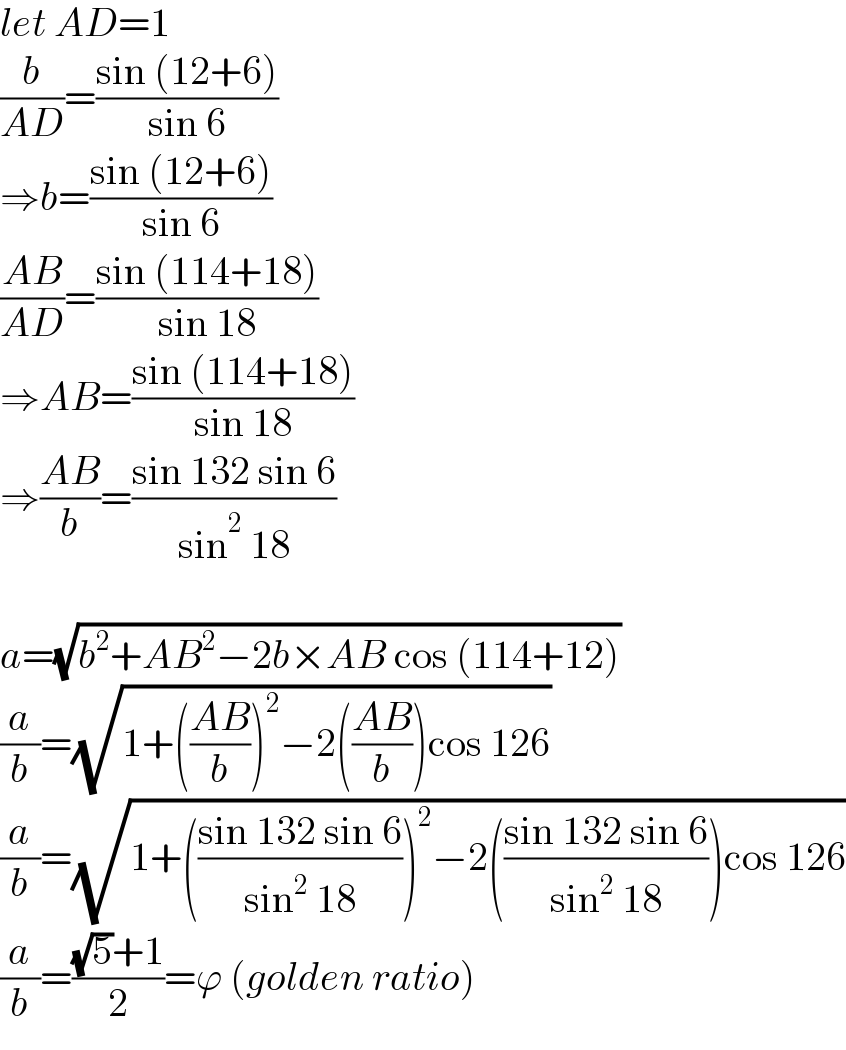
$${let}\:{AD}=\mathrm{1} \\ $$$$\frac{{b}}{{AD}}=\frac{\mathrm{sin}\:\left(\mathrm{12}+\mathrm{6}\right)}{\mathrm{sin}\:\mathrm{6}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{sin}\:\left(\mathrm{12}+\mathrm{6}\right)}{\mathrm{sin}\:\mathrm{6}} \\ $$$$\frac{{AB}}{{AD}}=\frac{\mathrm{sin}\:\left(\mathrm{114}+\mathrm{18}\right)}{\mathrm{sin}\:\mathrm{18}} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{sin}\:\left(\mathrm{114}+\mathrm{18}\right)}{\mathrm{sin}\:\mathrm{18}} \\ $$$$\Rightarrow\frac{{AB}}{{b}}=\frac{\mathrm{sin}\:\mathrm{132}\:\mathrm{sin}\:\mathrm{6}}{\mathrm{sin}^{\mathrm{2}} \:\mathrm{18}} \\ $$$$ \\ $$$${a}=\sqrt{{b}^{\mathrm{2}} +{AB}^{\mathrm{2}} −\mathrm{2}{b}×{AB}\:\mathrm{cos}\:\left(\mathrm{114}+\mathrm{12}\right)} \\ $$$$\frac{{a}}{{b}}=\sqrt{\mathrm{1}+\left(\frac{{AB}}{{b}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{AB}}{{b}}\right)\mathrm{cos}\:\mathrm{126}} \\ $$$$\frac{{a}}{{b}}=\sqrt{\mathrm{1}+\left(\frac{\mathrm{sin}\:\mathrm{132}\:\mathrm{sin}\:\mathrm{6}}{\mathrm{sin}^{\mathrm{2}} \:\mathrm{18}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{sin}\:\mathrm{132}\:\mathrm{sin}\:\mathrm{6}}{\mathrm{sin}^{\mathrm{2}} \:\mathrm{18}}\right)\mathrm{cos}\:\mathrm{126}} \\ $$$$\frac{{a}}{{b}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}=\varphi\:\left({golden}\:{ratio}\right) \\ $$
Commented by MathSh last updated on 19/Oct/21
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{solution}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Ser} \\ $$
