Question Number 157055 by cortano last updated on 19/Oct/21

Commented by MathSh last updated on 20/Oct/21
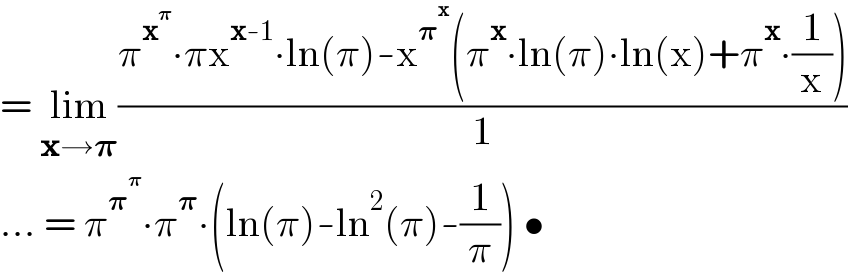
$$=\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\boldsymbol{\pi}} {\mathrm{lim}}\frac{\pi^{\boldsymbol{\mathrm{x}}^{\boldsymbol{\pi}} } \centerdot\pi\mathrm{x}^{\boldsymbol{\mathrm{x}}-\mathrm{1}} \centerdot\mathrm{ln}\left(\pi\right)-\mathrm{x}^{\boldsymbol{\pi}^{\boldsymbol{\mathrm{x}}} } \left(\pi^{\boldsymbol{\mathrm{x}}} \centerdot\mathrm{ln}\left(\pi\right)\centerdot\mathrm{ln}\left(\mathrm{x}\right)+\pi^{\boldsymbol{\mathrm{x}}} \centerdot\frac{\mathrm{1}}{\mathrm{x}}\right)}{\mathrm{1}} \\ $$$$…\:=\:\pi^{\boldsymbol{\pi}^{\boldsymbol{\pi}} } \centerdot\pi^{\boldsymbol{\pi}} \centerdot\left(\mathrm{ln}\left(\pi\right)-\mathrm{ln}^{\mathrm{2}} \left(\pi\right)-\frac{\mathrm{1}}{\pi}\right)\:\bullet \\ $$
Answered by mathlove last updated on 19/Oct/21

$$ \\ $$
