Menu Close

Question-157175

Tinku Tara 0 Comments
Pin




Question Number 157175 by cortano last updated on 20/Oct/21
Commented by puissant last updated on 20/Oct/21
Ω=(π^2 /4)
$$\Omega=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
Answered by Mathspace last updated on 20/Oct/21
I=∫_0 ^∞ ln(((1+e^(−x) )/(1−e^(−x) )))dx =∫_0 ^∞ ln(1+e^(−x) )dx−∫_0 ^∞ ln(1−e^(−x)) dx ln^′ (1+u)dx=(1/(1+u))=Σ(−1)^n u^n ⇒ ln(1+u)=Σ_(n=0) ^∞ (−1)^n (u^(n+1) /(n+1)) =Σ_(n=1) ^(∞ ) (−1)^(n−1 ) (u^n /n) ⇒ ln(1+e^(−x) )=Σ_(n=1) ^∞ (−1)^(n−1) (e^(−nx) /n) and ∫_0 ^∞ ln(1+e^(−x) )dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^∞ e^(−nx) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)(−(1/n))[e^(−nx) ]_0 ^∞ =−Σ_(n=1) ^∞ (((−1)^n )/n^2 )=−δ(2) =−(2^(1−2) −1)ξ(2) =−((1/2)−1)×(π^2 /6)=(π^2 /(12)) ln^′ (1−u)=−(1/(1−u))=−Σ_(n=0) ^∞ u^(n ) ⇒ ln(1−u)=−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (u^n /n) ⇒ln(1−e^(−x) ) =−Σ_(n=1) ^∞ (e^(−nx) /n) ⇒ ∫_0 ^∞ ln(1−e^(−x) )dx =−Σ_(n=1) ^∞ (1/n)∫_0 ^∞ e^(−nx) dx =−Σ_(n=1) ^∞ (1/n)[−(1/n)e^(−nx) ]_0 ^∞ =−Σ_(n=1) ^∞ (1/n^2 )=−(π^2 /6) ⇒ I=(π^2 /(12))+(π^2 /6)=((3π^2 )/(12))⇒I=(π^2 /4)
$${I}=\int_{\mathrm{0}} ^{\infty} {ln}\left(\frac{\mathrm{1}+{e}^{−{x}} }{\mathrm{1}−{e}^{−{x}} }\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{e}^{−{x}} \right){dx}−\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}−{e}^{\left.−{x}\right)} {dx}\right. \\ $$$${ln}^{'} \left(\mathrm{1}+{u}\right){dx}=\frac{\mathrm{1}}{\mathrm{1}+{u}}=\Sigma\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty\:} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}\:} \frac{{u}^{{n}} }{{n}}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{e}^{−{x}} \right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\frac{{e}^{−{nx}} }{{n}} \\ $$$${and}\:\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{e}^{−{x}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{nx}} {dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\left(−\frac{\mathrm{1}}{{n}}\right)\left[{e}^{−{nx}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }=−\delta\left(\mathrm{2}\right) \\ $$$$=−\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right) \\ $$$$=−\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$${ln}^{'} \left(\mathrm{1}−{u}\right)=−\frac{\mathrm{1}}{\mathrm{1}−{u}}=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}\:} \Rightarrow \\ $$$${ln}\left(\mathrm{1}−{u}\right)=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\Rightarrow{ln}\left(\mathrm{1}−{e}^{−{x}} \right) \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{e}^{−{nx}} }{{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}−{e}^{−{x}} \right){dx} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\infty} {e}^{−{nx}} {dx} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}}\left[−\frac{\mathrm{1}}{{n}}{e}^{−{nx}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{12}}\Rightarrow{I}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
Answered by Mathspace last updated on 20/Oct/21
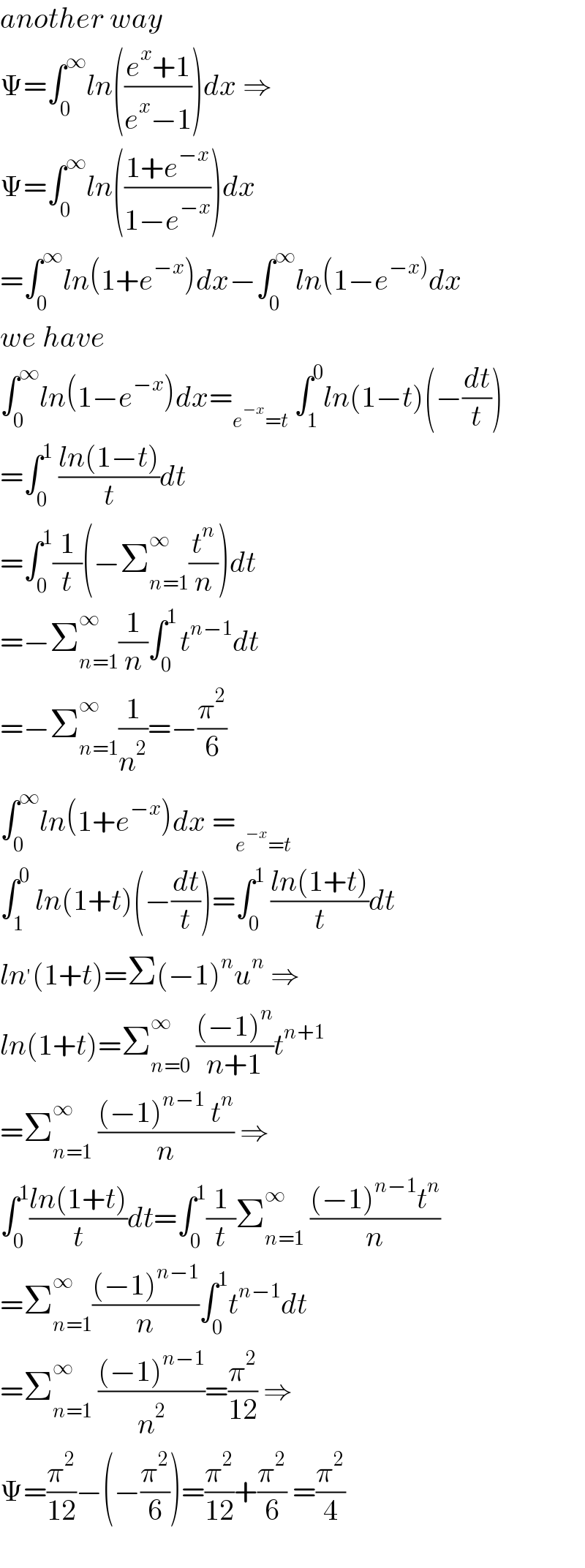
another way Ψ=∫_0 ^∞ ln(((e^x +1)/(e^x −1)))dx ⇒ Ψ=∫_0 ^∞ ln(((1+e^(−x) )/(1−e^(−x) )))dx =∫_0 ^∞ ln(1+e^(−x) )dx−∫_0 ^∞ ln(1−e^(−x)) dx we have ∫_0 ^∞ ln(1−e^(−x) )dx=_(e^(−x) =t) ∫_1 ^0 ln(1−t)(−(dt/t)) =∫_0 ^1 ((ln(1−t))/t)dt =∫_0 ^1 (1/t)(−Σ_(n=1) ^(∞ ) (t^n /n))dt =−Σ_(n=1) ^(∞ ) (1/n)∫_0 ^(1 ) t^(n−1) dt =−Σ_(n=1) ^(∞ ) (1/n^2 )=−(π^2 /6) ∫_0 ^∞ ln(1+e^(−x) )dx =_(e^(−x) =t) ∫_1 ^0 ln(1+t)(−(dt/t))=∫_0 ^1 ((ln(1+t))/t)dt ln^′ (1+t)=Σ(−1)^n u^n ⇒ ln(1+t)=Σ_(n=0) ^∞ (((−1)^n )/(n+1))t^(n+1) =Σ_(n=1) ^∞ (((−1)^(n−1) t^n )/n) ⇒ ∫_0 ^1 ((ln(1+t))/t)dt=∫_0 ^1 (1/t)Σ_(n=1) ^∞ (((−1)^(n−1) t^n )/n) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 t^(n−1) dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )=(π^2 /(12)) ⇒ Ψ=(π^2 /(12))−(−(π^2 /6))=(π^2 /(12))+(π^2 /6) =(π^2 /4)
$${another}\:{way} \\ $$$$\Psi=\int_{\mathrm{0}} ^{\infty} {ln}\left(\frac{{e}^{{x}} +\mathrm{1}}{{e}^{{x}} −\mathrm{1}}\right){dx}\:\Rightarrow \\ $$$$\Psi=\int_{\mathrm{0}} ^{\infty} {ln}\left(\frac{\mathrm{1}+{e}^{−{x}} }{\mathrm{1}−{e}^{−{x}} }\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{e}^{−{x}} \right){dx}−\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}−{e}^{\left.−{x}\right)} {dx}\right. \\ $$$${we}\:{have}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}−{e}^{−{x}} \right){dx}=_{{e}^{−{x}} ={t}} \:\int_{\mathrm{1}} ^{\mathrm{0}} {ln}\left(\mathrm{1}−{t}\right)\left(−\frac{{dt}}{{t}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}}\left(−\sum_{{n}=\mathrm{1}} ^{\infty\:} \frac{{t}^{{n}} }{{n}}\right){dt} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty\:} \frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}\:} {t}^{{n}−\mathrm{1}} {dt} \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty\:} \frac{\mathrm{1}}{{n}^{\mathrm{2}} }=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+{e}^{−{x}} \right){dx}\:=_{{e}^{−{x}} ={t}} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{0}} \:{ln}\left(\mathrm{1}+{t}\right)\left(−\frac{{dt}}{{t}}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}{dt} \\ $$$${ln}^{'} \left(\mathrm{1}+{t}\right)=\Sigma\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{t}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{t}^{{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{t}^{{n}} }{{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {t}^{{n}} }{{n}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}−\mathrm{1}} {dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\Rightarrow \\ $$$$\Psi=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\left(−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *