Menu Close

Question-157196

Tinku Tara 0 Comments
Pin




Question Number 157196 by MathSh last updated on 20/Oct/21
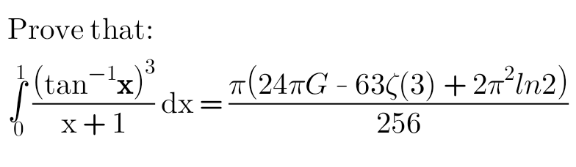
Answered by mindispower last updated on 21/Oct/21
(π^3 /(64))ln(2)−3∫_0 ^1 ((ln(1+x))/(1+x^2 ))tan^(−1) (x)^2 dx =−3∫_0 ^(π/4) ln(1+tg(t))t^2 dtt ∫_0 ^(π/4) ln(1+tg(t))t^2 dt=∫_0 ^(π/4) ln(1+tg((π/4)−t))((π/4)−t)^2 ⇒2∫_0 ^(π/4) ln(1+tg(t))t^2 dt=∫_0 ^(π/4) ln(2)t^2 −(π^2 /(16))∫_0 ^(π/4) ln(1+tan(t))dt +(π/2)∫_0 ^(π/4) tln(1+tg(t))dt =A−(π^2 /(16))B+(π/2)C A=((ln(2))/3)((π^3 /(64))) C=∫_0 ^(π/4) ln((((√2)sin((π/4)+x))/(cos(x))))tdt =−2∫_0 ^(π/4) ln(cos(t))tdt_(=Y) +((ln((√2)))/2).(π/4) Y=2∫_0 ^(π/4) Σ_(k≥1) (−1)^k ((cos(2kx))/k)xdx+2∫_0 ^(π/4) ln(2)tdt =2Σ_(k≥1) (((−1)^k )/k)[(π/(8k))sin(((kπ)/2))+((cos(((kπ)/2))−1)/(4k^2 ))]+((ln(2)π^2 )/(16)) =−2Σ_(k≥0) (((−1)^k π)/(8(2k+1)^2 ))−(1/2)Σ_(k≥1) (((−1)^k )/k^3 )+(1/2)Σ_(k≥1) (((−1)^k )/(8k^3 ))+((ln(2)π^2 )/(16)) −2((π/8)C−((21)/(128))ζ(3)−(π^2 /(32))ln(2)) =−2(((16πC−21ζ(3)−4π^2 ln(2))/(128)))+((πln(2))/(32)) ∫_0 ^(π/4) ln(1+tg(t))dt=B =∫_0 ^(π/4) ln((2/(1+tg(t))))=B ⇔B=(π/8)ln(2) A=((ln(2))/3).(π^3 /(64)) ∫_0 ^(π/4) t^2 ln(1+tan(t))dt=(1/2)(((ln(2))/3).(π^3 /(64))−(π^2 /(16))(((πln(2))/8))−2π(((16πC−21ζ(3)−4π^2 ln(2))/(128)))+(π^2 /2).((ln(2))/(32)))=Ω ∫_0 ^(1() ((tan^− (x))^3 )/(1+x))dx=((π^3 ln(2))/(64))−3Ω
$$\frac{\pi^{\mathrm{3}} }{\mathrm{64}}{ln}\left(\mathrm{2}\right)−\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{tan}^{−\mathrm{1}} \left({x}\right)^{\mathrm{2}} {dx} \\ $$$$=−\mathrm{3}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tg}\left({t}\right)\right){t}^{\mathrm{2}} {dtt} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tg}\left({t}\right)\right){t}^{\mathrm{2}} {dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tg}\left(\frac{\pi}{\mathrm{4}}−{t}\right)\right)\left(\frac{\pi}{\mathrm{4}}−{t}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tg}\left({t}\right)\right){t}^{\mathrm{2}} {dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{2}\right){t}^{\mathrm{2}} −\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tan}\left({t}\right)\right){dt} \\ $$$$+\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tln}\left(\mathrm{1}+{tg}\left({t}\right)\right){dt} \\ $$$$={A}−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}{B}+\frac{\pi}{\mathrm{2}}{C} \\ $$$${A}=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\left(\frac{\pi^{\mathrm{3}} }{\mathrm{64}}\right) \\ $$$${C}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\sqrt{\mathrm{2}}{sin}\left(\frac{\pi}{\mathrm{4}}+{x}\right)}{{cos}\left({x}\right)}\right){tdt} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({t}\right)\right){td}\underset{={Y}} {{t}}+\frac{{ln}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}}.\frac{\pi}{\mathrm{4}} \\ $$$${Y}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \underset{{k}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{k}} \frac{{cos}\left(\mathrm{2}{kx}\right)}{{k}}{xdx}+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{2}\right){tdt} \\ $$$$=\mathrm{2}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\left[\frac{\pi}{\mathrm{8}{k}}{sin}\left(\frac{{k}\pi}{\mathrm{2}}\right)+\frac{{cos}\left(\frac{{k}\pi}{\mathrm{2}}\right)−\mathrm{1}}{\mathrm{4}{k}^{\mathrm{2}} }\right]+\frac{{ln}\left(\mathrm{2}\right)\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$$$=−\mathrm{2}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} \pi}{\mathrm{8}\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{8}{k}^{\mathrm{3}} }+\frac{{ln}\left(\mathrm{2}\right)\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$$$−\mathrm{2}\left(\frac{\pi}{\mathrm{8}}{C}−\frac{\mathrm{21}}{\mathrm{128}}\zeta\left(\mathrm{3}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{32}}{ln}\left(\mathrm{2}\right)\right) \\ $$$$=−\mathrm{2}\left(\frac{\mathrm{16}\pi{C}−\mathrm{21}\zeta\left(\mathrm{3}\right)−\mathrm{4}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{128}}\right)+\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{32}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tg}\left({t}\right)\right){dt}={B} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{\mathrm{2}}{\mathrm{1}+{tg}\left({t}\right)}\right)={B} \\ $$$$\Leftrightarrow{B}=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right) \\ $$$${A}=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}.\frac{\pi^{\mathrm{3}} }{\mathrm{64}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {t}^{\mathrm{2}} {ln}\left(\mathrm{1}+{tan}\left({t}\right)\right){dt}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}.\frac{\pi^{\mathrm{3}} }{\mathrm{64}}−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\left(\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}}\right)−\mathrm{2}\pi\left(\frac{\mathrm{16}\pi{C}−\mathrm{21}\zeta\left(\mathrm{3}\right)−\mathrm{4}\pi^{\mathrm{2}} {ln}\left(\mathrm{2}\right)}{\mathrm{128}}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{2}}.\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{32}}\right)=\Omega \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}\left(\right.} \frac{\left.{tan}^{−} \left({x}\right)\right)^{\mathrm{3}} }{\mathrm{1}+{x}}{dx}=\frac{\pi^{\mathrm{3}} {ln}\left(\mathrm{2}\right)}{\mathrm{64}}−\mathrm{3}\Omega \\ $$$$ \\ $$$$ \\ $$
Commented by MathSh last updated on 21/Oct/21
Perfect dear Ser, thank you so much
$$\mathrm{Perfect}\:\mathrm{dear}\:\mathrm{Ser},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *