Question-157209

Question Number 157209 by aliyn last updated on 21/Oct/21

Commented by aliyn last updated on 21/Oct/21

$${prove}\:{this}\:?? \\ $$

Commented by cortano last updated on 21/Oct/21

$$\:{a}^{\mathrm{log}\:_{{a}} \:{b}} \:=\:{b}^{\mathrm{log}\:_{{a}} {a}} \:=\:{b}\: \\ $$$$\:\left[\:\mathrm{log}\:_{{a}} {a}\:=\mathrm{1}\:\right] \\ $$

Answered by puissant last updated on 21/Oct/21

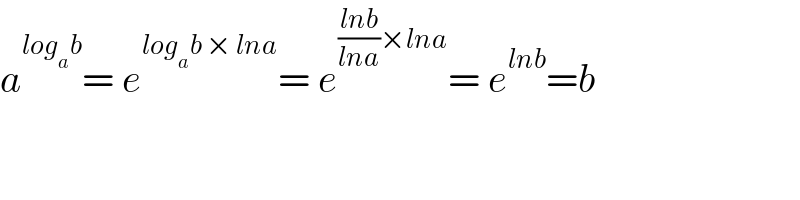
$${a}^{{log}_{{a}} {b}} =\:{e}^{{log}_{{a}} {b}\:×\:{lna}} =\:{e}^{\frac{{lnb}}{{lna}}×{lna}} =\:{e}^{{lnb}} ={b} \\ $$

Answered by mr W last updated on 21/Oct/21

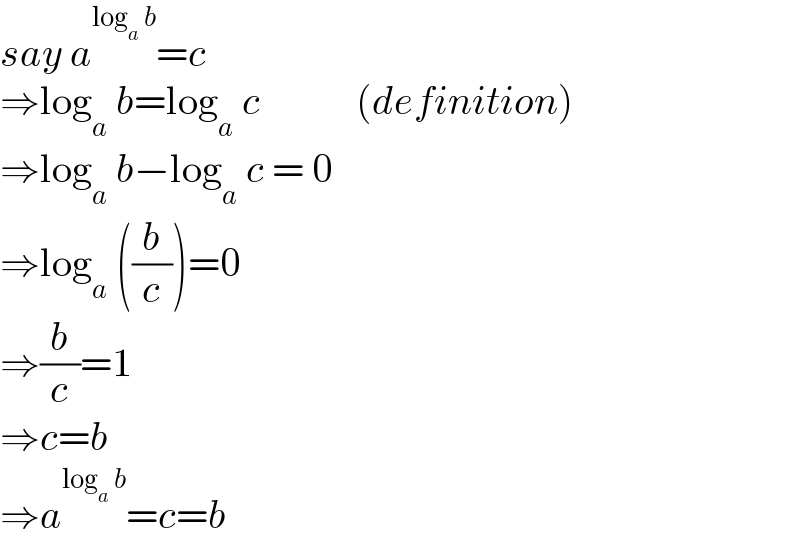
$${say}\:{a}^{\mathrm{log}_{{a}} \:{b}} ={c} \\ $$$$\Rightarrow\mathrm{log}_{{a}} \:{b}=\mathrm{log}_{{a}} \:{c}\:\:\:\:\:\:\:\:\:\:\:\:\left({definition}\right) \\ $$$$\Rightarrow\mathrm{log}_{{a}} \:{b}−\mathrm{log}_{{a}} \:{c}\:=\:\mathrm{0}\:\: \\ $$$$\Rightarrow\mathrm{log}_{{a}} \:\left(\frac{{b}}{{c}}\right)=\mathrm{0} \\ $$$$\Rightarrow\frac{{b}}{{c}}=\mathrm{1} \\ $$$$\Rightarrow{c}={b} \\ $$$$\Rightarrow{a}^{\mathrm{log}_{{a}} \:{b}} ={c}={b} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com