Question Number 157222 by amin96 last updated on 21/Oct/21

Answered by Dimitri_01 last updated on 21/Oct/21
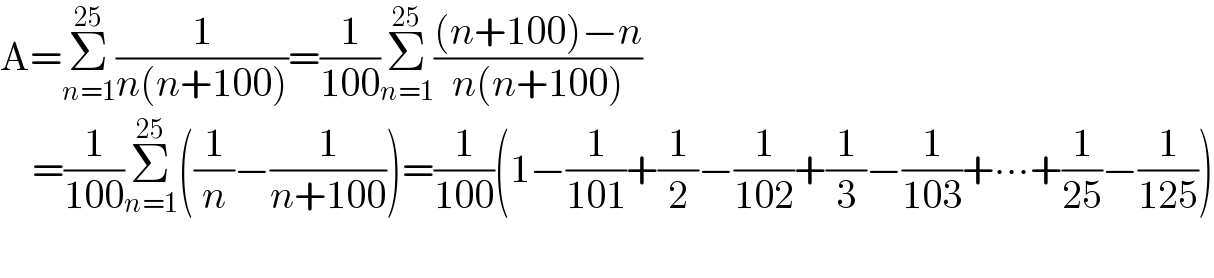
$$\mathrm{A}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{25}} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{100}\right)}=\frac{\mathrm{1}}{\mathrm{100}}\underset{{n}=\mathrm{1}} {\overset{\mathrm{25}} {\sum}}\frac{\left({n}+\mathrm{100}\right)−{n}}{{n}\left({n}+\mathrm{100}\right)} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{100}}\underset{{n}=\mathrm{1}} {\overset{\mathrm{25}} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{100}}\right)=\frac{\mathrm{1}}{\mathrm{100}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{101}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{102}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{103}}+\centerdot\centerdot\centerdot+\frac{\mathrm{1}}{\mathrm{25}}−\frac{\mathrm{1}}{\mathrm{125}}\right) \\ $$$$ \\ $$
Answered by qaz last updated on 21/Oct/21
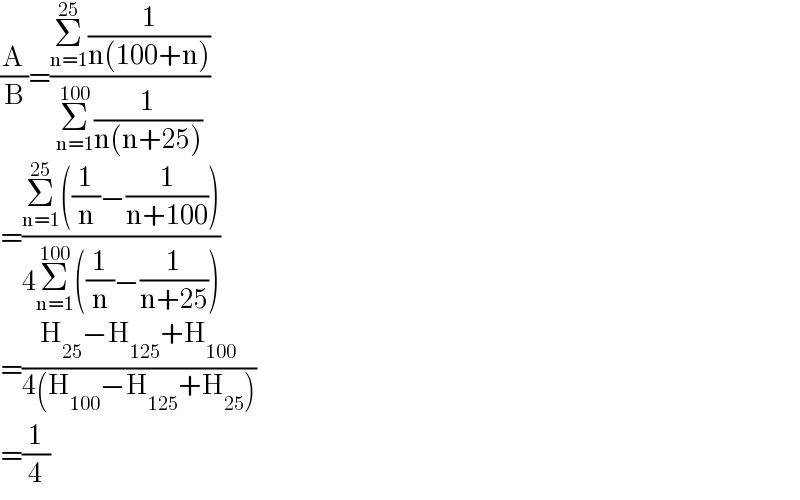
$$\frac{\mathrm{A}}{\mathrm{B}}=\frac{\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{25}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{100}+\mathrm{n}\right)}}{\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{25}\right)}} \\ $$$$=\frac{\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{25}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{100}}\right)}{\mathrm{4}\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{25}}\right)} \\ $$$$=\frac{\mathrm{H}_{\mathrm{25}} −\mathrm{H}_{\mathrm{125}} +\mathrm{H}_{\mathrm{100}} }{\mathrm{4}\left(\mathrm{H}_{\mathrm{100}} −\mathrm{H}_{\mathrm{125}} +\mathrm{H}_{\mathrm{25}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by Tawa11 last updated on 21/Oct/21

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
