Menu Close

Question-157223

Tinku Tara 0 Comments
Pin




Question Number 157223 by amin96 last updated on 21/Oct/21
Answered by Rasheed.Sindhi last updated on 21/Oct/21
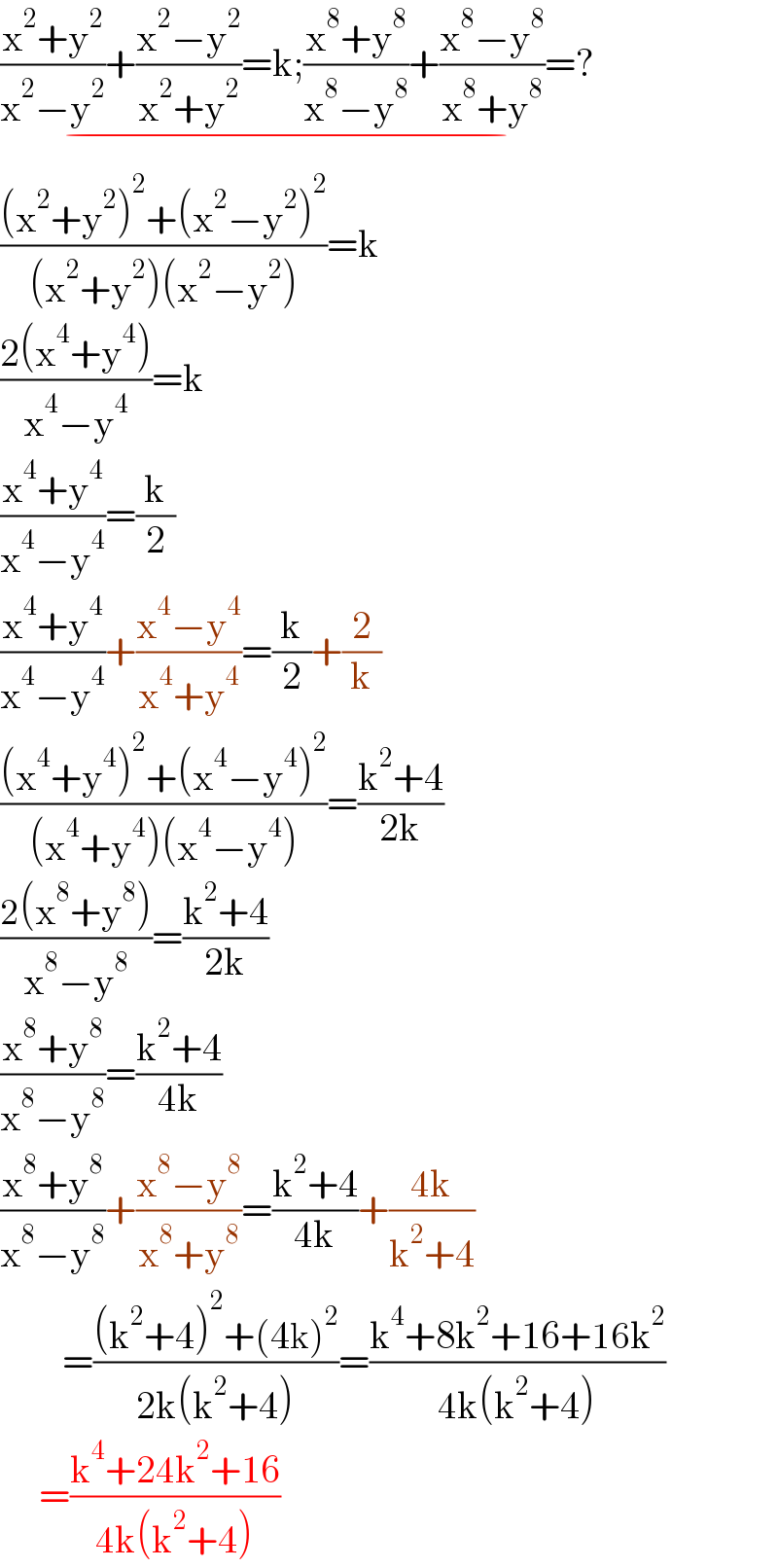
((x^2 +y^2 )/(x^2 −y^2 ))+((x^2 −y^2 )/(x^2 +y^2 ))=k;((x^8 +y^8 )/(x^8 −y^8 ))+((x^8 −y^8 )/(x^8 +y^8 ))=?_(−) (((x^2 +y^2 )^2 +(x^2 −y^2 )^2 )/((x^2 +y^2 )(x^2 −y^2 )))=k ((2(x^4 +y^4 ))/(x^4 −y^4 ))=k ((x^4 +y^4 )/(x^4 −y^4 ))=(k/2) ((x^4 +y^4 )/(x^4 −y^4 ))+((x^4 −y^4 )/(x^4 +y^4 ))=(k/2)+(2/k) (((x^4 +y^4 )^2 +(x^4 −y^4 )^2 )/((x^4 +y^4 )(x^4 −y^4 )))=((k^2 +4)/(2k)) ((2(x^8 +y^8 ))/(x^8 −y^8 ))=((k^2 +4)/(2k)) ((x^8 +y^8 )/(x^8 −y^8 ))=((k^2 +4)/(4k)) ((x^8 +y^8 )/(x^8 −y^8 ))+((x^8 −y^8 )/(x^8 +y^8 ))=((k^2 +4)/(4k))+((4k)/(k^2 +4)) =(((k^2 +4)^2 +(4k)^2 )/(2k(k^2 +4)))=((k^4 +8k^2 +16+16k^2 )/(4k(k^2 +4))) =((k^4 +24k^2 +16)/(4k(k^2 +4)))
$$\underset{−} {\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }+\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }=\mathrm{k};\frac{\mathrm{x}^{\mathrm{8}} +\mathrm{y}^{\mathrm{8}} }{\mathrm{x}^{\mathrm{8}} −\mathrm{y}^{\mathrm{8}} }+\frac{\mathrm{x}^{\mathrm{8}} −\mathrm{y}^{\mathrm{8}} }{\mathrm{x}^{\mathrm{8}} +\mathrm{y}^{\mathrm{8}} }=?} \\ $$$$\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)}=\mathrm{k} \\ $$$$\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} \right)}{\mathrm{x}^{\mathrm{4}} −\mathrm{y}^{\mathrm{4}} }=\mathrm{k} \\ $$$$\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{4}} −\mathrm{y}^{\mathrm{4}} }=\frac{\mathrm{k}}{\mathrm{2}} \\ $$$$\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{4}} −\mathrm{y}^{\mathrm{4}} }+\frac{\mathrm{x}^{\mathrm{4}} −\mathrm{y}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} }=\frac{\mathrm{k}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{k}} \\ $$$$\frac{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} \right)^{\mathrm{2}} +\left(\mathrm{x}^{\mathrm{4}} −\mathrm{y}^{\mathrm{4}} \right)^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} \right)\left(\mathrm{x}^{\mathrm{4}} −\mathrm{y}^{\mathrm{4}} \right)}=\frac{\mathrm{k}^{\mathrm{2}} +\mathrm{4}}{\mathrm{2k}} \\ $$$$\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{8}} +\mathrm{y}^{\mathrm{8}} \right)}{\mathrm{x}^{\mathrm{8}} −\mathrm{y}^{\mathrm{8}} }=\frac{\mathrm{k}^{\mathrm{2}} +\mathrm{4}}{\mathrm{2k}} \\ $$$$\frac{\mathrm{x}^{\mathrm{8}} +\mathrm{y}^{\mathrm{8}} }{\mathrm{x}^{\mathrm{8}} −\mathrm{y}^{\mathrm{8}} }=\frac{\mathrm{k}^{\mathrm{2}} +\mathrm{4}}{\mathrm{4k}} \\ $$$$\frac{\mathrm{x}^{\mathrm{8}} +\mathrm{y}^{\mathrm{8}} }{\mathrm{x}^{\mathrm{8}} −\mathrm{y}^{\mathrm{8}} }+\frac{\mathrm{x}^{\mathrm{8}} −\mathrm{y}^{\mathrm{8}} }{\mathrm{x}^{\mathrm{8}} +\mathrm{y}^{\mathrm{8}} }=\frac{\mathrm{k}^{\mathrm{2}} +\mathrm{4}}{\mathrm{4k}}+\frac{\mathrm{4k}}{\mathrm{k}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{k}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{4k}\right)^{\mathrm{2}} }{\mathrm{2k}\left(\mathrm{k}^{\mathrm{2}} +\mathrm{4}\right)}=\frac{\mathrm{k}^{\mathrm{4}} +\mathrm{8k}^{\mathrm{2}} +\mathrm{16}+\mathrm{16k}^{\mathrm{2}} }{\mathrm{4k}\left(\mathrm{k}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$$$\:\:\:\:\:=\frac{\mathrm{k}^{\mathrm{4}} +\mathrm{24k}^{\mathrm{2}} +\mathrm{16}}{\mathrm{4k}\left(\mathrm{k}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$
Answered by som(math1967) last updated on 21/Oct/21
(((x^2 +y^2 )^2 +(x^2 −y^2 )^2 )/((x^2 −y^2 )(x^2 +y^2 )))=k ⇒((x^4 +y^4 )/(x^4 −y^4 ))=(k/2) ⇒((x^4 +y^4 +x^4 −y^4 )/(x^4 +y^4 −x^4 +y^4 ))=((k+2)/(k−2))★ ⇒(x^8 /y^8 )=(((k+2)/(k−2)))^2 ⇒((x^8 +y^8 )/(x^8 −y^8 ))=((2(k^2 +4))/(8k)) ★ ∴((x^8 +y^8 )/(x^8 −y^8 )) + ((x^8 −y^8 )/(x^8 +y^8 ))=((k^2 +4)/(4k))+((4k)/(k^2 +4)) =((k^4 +24k^2 +16)/(4k(k^2 +4))) ★if (a/b)=(c/d) then ((a+b)/(a−b))=((c+d)/(c−d)) componendo and dividendo
$$\frac{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}={k} \\ $$$$\Rightarrow\frac{{x}^{\mathrm{4}} +{y}^{\mathrm{4}} }{{x}^{\mathrm{4}} −{y}^{\mathrm{4}} }=\frac{{k}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{x}^{\mathrm{4}} −{y}^{\mathrm{4}} }{{x}^{\mathrm{4}} +{y}^{\mathrm{4}} −{x}^{\mathrm{4}} +{y}^{\mathrm{4}} }=\frac{{k}+\mathrm{2}}{{k}−\mathrm{2}}\bigstar \\ $$$$\Rightarrow\frac{{x}^{\mathrm{8}} }{{y}^{\mathrm{8}} }=\left(\frac{{k}+\mathrm{2}}{{k}−\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{x}^{\mathrm{8}} +{y}^{\mathrm{8}} }{{x}^{\mathrm{8}} −{y}^{\mathrm{8}} }=\frac{\mathrm{2}\left({k}^{\mathrm{2}} +\mathrm{4}\right)}{\mathrm{8}{k}}\:\bigstar \\ $$$$\therefore\frac{{x}^{\mathrm{8}} +{y}^{\mathrm{8}} }{{x}^{\mathrm{8}} −{y}^{\mathrm{8}} }\:+\:\frac{{x}^{\mathrm{8}} −{y}^{\mathrm{8}} }{{x}^{\mathrm{8}} +{y}^{\mathrm{8}} }=\frac{{k}^{\mathrm{2}} +\mathrm{4}}{\mathrm{4}{k}}+\frac{\mathrm{4}{k}}{{k}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\:\:\:\:=\frac{{k}^{\mathrm{4}} +\mathrm{24}{k}^{\mathrm{2}} +\mathrm{16}}{\mathrm{4}{k}\left({k}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$$$\bigstar{if}\:\frac{{a}}{{b}}=\frac{{c}}{{d}}\:{then}\:\frac{{a}+{b}}{{a}−{b}}=\frac{{c}+{d}}{{c}−{d}} \\ $$$${componendo}\:{and}\:{dividendo} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *