Question Number 157225 by mr W last updated on 21/Oct/21

Commented by mr W last updated on 21/Oct/21
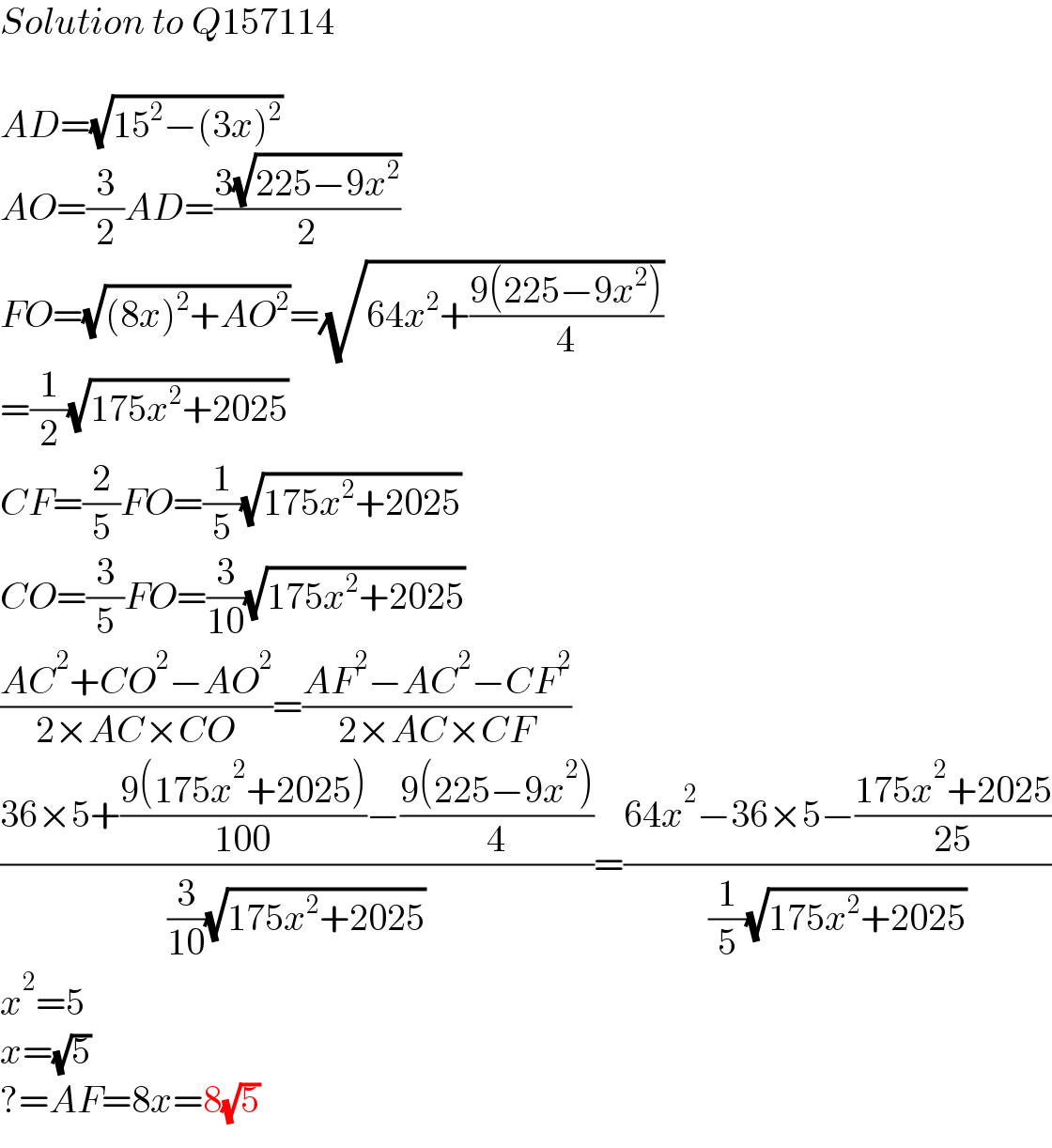
$${Solution}\:{to}\:{Q}\mathrm{157114} \\ $$$$ \\ $$$${AD}=\sqrt{\mathrm{15}^{\mathrm{2}} −\left(\mathrm{3}{x}\right)^{\mathrm{2}} } \\ $$$${AO}=\frac{\mathrm{3}}{\mathrm{2}}{AD}=\frac{\mathrm{3}\sqrt{\mathrm{225}−\mathrm{9}{x}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${FO}=\sqrt{\left(\mathrm{8}{x}\right)^{\mathrm{2}} +{AO}^{\mathrm{2}} }=\sqrt{\mathrm{64}{x}^{\mathrm{2}} +\frac{\mathrm{9}\left(\mathrm{225}−\mathrm{9}{x}^{\mathrm{2}} \right)}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{175}{x}^{\mathrm{2}} +\mathrm{2025}} \\ $$$${CF}=\frac{\mathrm{2}}{\mathrm{5}}{FO}=\frac{\mathrm{1}}{\mathrm{5}}\sqrt{\mathrm{175}{x}^{\mathrm{2}} +\mathrm{2025}} \\ $$$${CO}=\frac{\mathrm{3}}{\mathrm{5}}{FO}=\frac{\mathrm{3}}{\mathrm{10}}\sqrt{\mathrm{175}{x}^{\mathrm{2}} +\mathrm{2025}} \\ $$$$\frac{{AC}^{\mathrm{2}} +{CO}^{\mathrm{2}} −{AO}^{\mathrm{2}} }{\mathrm{2}×{AC}×{CO}}=\frac{{AF}^{\mathrm{2}} −{AC}^{\mathrm{2}} −{CF}^{\mathrm{2}} }{\mathrm{2}×{AC}×{CF}} \\ $$$$\frac{\mathrm{36}×\mathrm{5}+\frac{\mathrm{9}\left(\mathrm{175}{x}^{\mathrm{2}} +\mathrm{2025}\right)}{\mathrm{100}}−\frac{\mathrm{9}\left(\mathrm{225}−\mathrm{9}{x}^{\mathrm{2}} \right)}{\mathrm{4}}}{\frac{\mathrm{3}}{\mathrm{10}}\sqrt{\mathrm{175}{x}^{\mathrm{2}} +\mathrm{2025}}}=\frac{\mathrm{64}{x}^{\mathrm{2}} −\mathrm{36}×\mathrm{5}−\frac{\mathrm{175}{x}^{\mathrm{2}} +\mathrm{2025}}{\mathrm{25}}}{\frac{\mathrm{1}}{\mathrm{5}}\sqrt{\mathrm{175}{x}^{\mathrm{2}} +\mathrm{2025}}} \\ $$$${x}^{\mathrm{2}} =\mathrm{5} \\ $$$${x}=\sqrt{\mathrm{5}} \\ $$$$?={AF}=\mathrm{8}{x}=\mathrm{8}\sqrt{\mathrm{5}} \\ $$
Commented by Tawa11 last updated on 21/Oct/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
