Question Number 157292 by mr W last updated on 21/Oct/21

Commented by mr W last updated on 21/Oct/21

Commented by mr W last updated on 21/Oct/21

$${Q}\mathrm{154599} \\ $$
Commented by ajfour last updated on 22/Oct/21
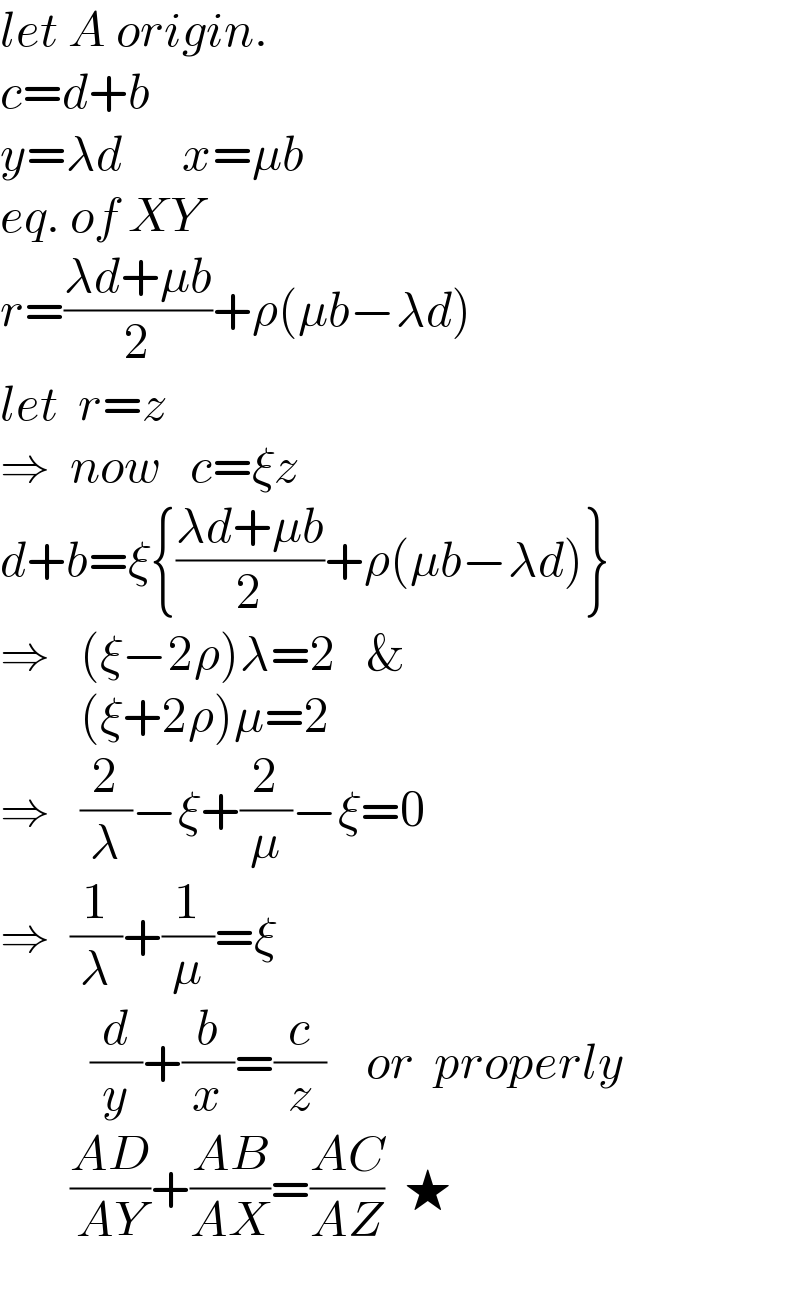
$${let}\:{A}\:{origin}. \\ $$$${c}={d}+{b} \\ $$$${y}=\lambda{d}\:\:\:\:\:\:{x}=\mu{b} \\ $$$${eq}.\:{of}\:{XY} \\ $$$${r}=\frac{\lambda{d}+\mu{b}}{\mathrm{2}}+\rho\left(\mu{b}−\lambda{d}\right) \\ $$$${let}\:\:{r}={z} \\ $$$$\Rightarrow\:\:{now}\:\:\:{c}=\xi{z} \\ $$$${d}+{b}=\xi\left\{\frac{\lambda{d}+\mu{b}}{\mathrm{2}}+\rho\left(\mu{b}−\lambda{d}\right)\right\} \\ $$$$\Rightarrow\:\:\:\left(\xi−\mathrm{2}\rho\right)\lambda=\mathrm{2}\:\:\:\& \\ $$$$\:\:\:\:\:\:\:\:\left(\xi+\mathrm{2}\rho\right)\mu=\mathrm{2} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{2}}{\lambda}−\xi+\frac{\mathrm{2}}{\mu}−\xi=\mathrm{0} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\lambda}+\frac{\mathrm{1}}{\mu}=\xi \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{d}}{{y}}+\frac{{b}}{{x}}=\frac{{c}}{{z}}\:\:\:\:{or}\:\:{properly} \\ $$$$\:\:\:\:\:\:\:\frac{{AD}}{{AY}}+\frac{{AB}}{{AX}}=\frac{{AC}}{{AZ}}\:\:\bigstar \\ $$$$ \\ $$
Commented by ajfour last updated on 22/Oct/21
https://youtu.be/BeqXQ4bPv14
Commented by ajfour last updated on 22/Oct/21
$${just}\:{my}\:{another}\:{dance}\:{cover}! \\ $$
Commented by mr W last updated on 22/Oct/21
$${great}\:{solution}\:{and}\:{great}\:{dance}! \\ $$
Answered by mr W last updated on 21/Oct/21

Commented by mr W last updated on 22/Oct/21
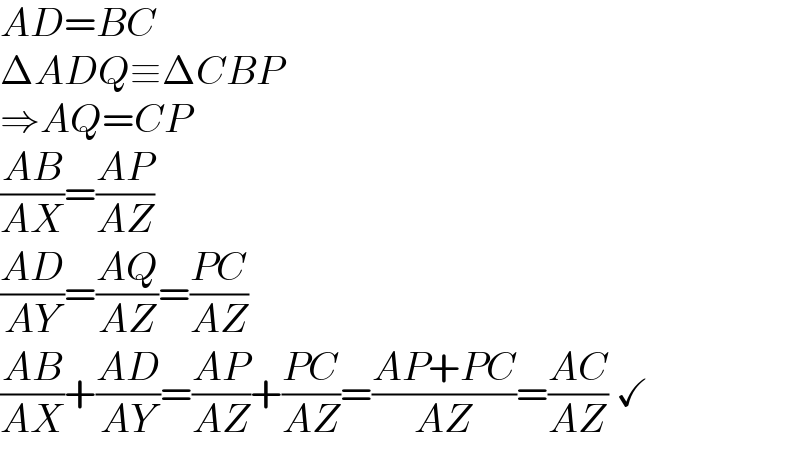
$${AD}={BC} \\ $$$$\Delta{ADQ}\equiv\Delta{CBP} \\ $$$$\Rightarrow{AQ}={CP} \\ $$$$\frac{{AB}}{{AX}}=\frac{{AP}}{{AZ}} \\ $$$$\frac{{AD}}{{AY}}=\frac{{AQ}}{{AZ}}=\frac{{PC}}{{AZ}} \\ $$$$\frac{{AB}}{{AX}}+\frac{{AD}}{{AY}}=\frac{{AP}}{{AZ}}+\frac{{PC}}{{AZ}}=\frac{{AP}+{PC}}{{AZ}}=\frac{{AC}}{{AZ}}\:\checkmark \\ $$
Commented by Tawa11 last updated on 21/Oct/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by ajfour last updated on 22/Oct/21

$${really} \\ $$
