Question Number 157382 by cortano last updated on 22/Oct/21

Answered by mr W last updated on 23/Oct/21
![g(x)=x+(1/x^2 ) g′(x)=1−(2/x^3 )=0 ⇒x=(2)^(1/3) ∈[1,2] g(x)_(min) =((3(2)^(1/3) )/( 2))=k f(x)=x^2 +ax+b=(x+(a/2))^2 +(b−(a^2 /4)) f(x)_(min) =b−(a^2 /4)=k=((3(2)^(1/3) )/2) f(x)_(max) =f(2)=4+2a+b=4+2a+(a^2 /4)+((3(2)^(1/3) )/2)](https://www.tinkutara.com/question/Q157501.png)
$${g}\left({x}\right)={x}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${g}'\left({x}\right)=\mathrm{1}−\frac{\mathrm{2}}{{x}^{\mathrm{3}} }=\mathrm{0}\:\Rightarrow{x}=\sqrt[{\mathrm{3}}]{\mathrm{2}}\:\in\left[\mathrm{1},\mathrm{2}\right] \\ $$$${g}\left({x}\right)_{{min}} =\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\:\mathrm{2}}={k} \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} +{ax}+{b}=\left({x}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({b}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$${f}\left({x}\right)_{{min}} ={b}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}={k}=\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}} \\ $$$${f}\left({x}\right)_{{max}} ={f}\left(\mathrm{2}\right)=\mathrm{4}+\mathrm{2}{a}+{b}=\mathrm{4}+\mathrm{2}{a}+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by cortano last updated on 24/Oct/21
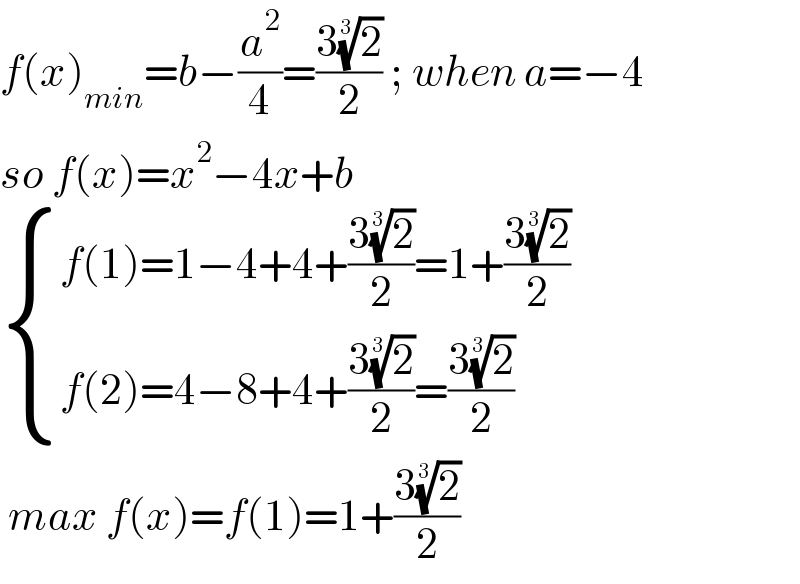
$${f}\left({x}\right)_{{min}} ={b}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}\:;\:{when}\:{a}=−\mathrm{4} \\ $$$${so}\:{f}\left({x}\right)={x}^{\mathrm{2}} −\mathrm{4}{x}+{b}\: \\ $$$$\begin{cases}{{f}\left(\mathrm{1}\right)=\mathrm{1}−\mathrm{4}+\mathrm{4}+\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}=\mathrm{1}+\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}}\\{{f}\left(\mathrm{2}\right)=\mathrm{4}−\mathrm{8}+\mathrm{4}+\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}}}\end{cases} \\ $$$$\:{max}\:{f}\left({x}\right)={f}\left(\mathrm{1}\right)=\mathrm{1}+\frac{\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{2}}}{\mathrm{2}} \\ $$
