Question Number 157392 by ajfour last updated on 22/Oct/21
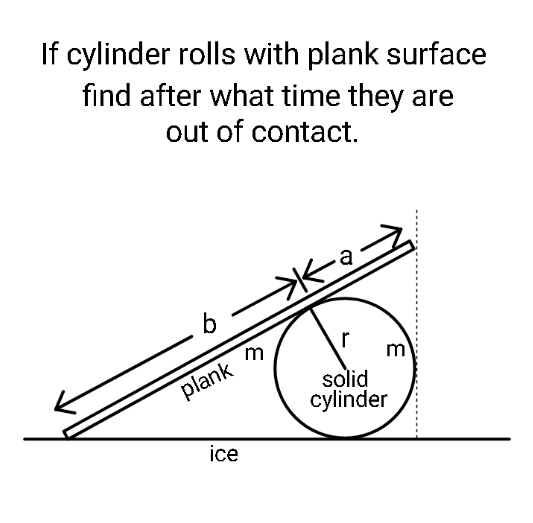
Commented by ajfour last updated on 22/Oct/21
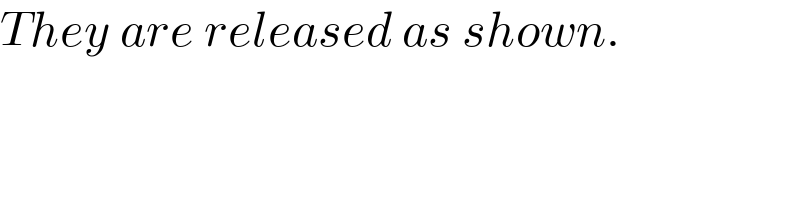
$${They}\:{are}\:{released}\:{as}\:{shown}. \\ $$
Commented by mr W last updated on 23/Oct/21

$${hard}\:{question}… \\ $$
Answered by ajfour last updated on 23/Oct/21
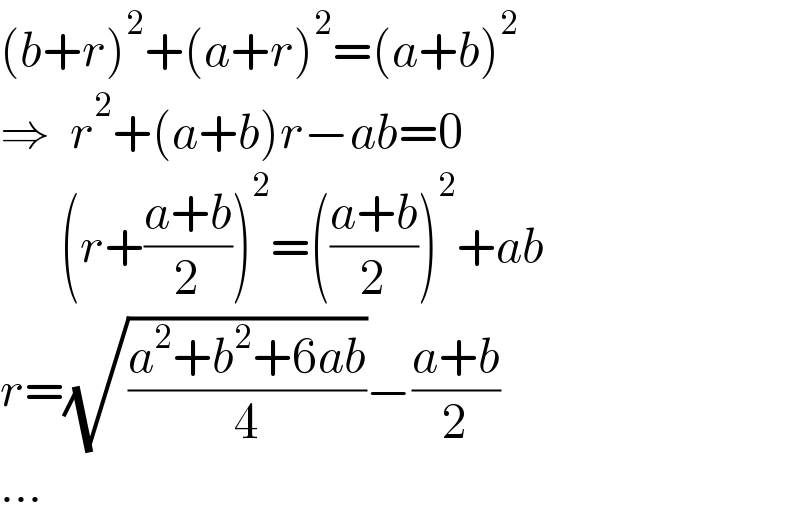
$$\left({b}+{r}\right)^{\mathrm{2}} +\left({a}+{r}\right)^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} +\left({a}+{b}\right){r}−{ab}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\left({r}+\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +{ab} \\ $$$${r}=\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{6}{ab}}{\mathrm{4}}}−\frac{{a}+{b}}{\mathrm{2}} \\ $$$$… \\ $$
