Question Number 157435 by MathSh last updated on 23/Oct/21
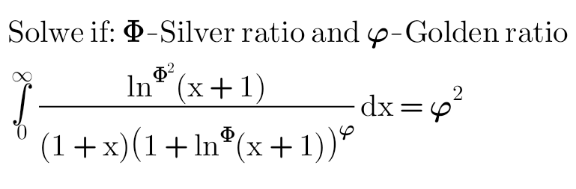
Answered by mindispower last updated on 23/Oct/21

$$\sim\frac{{ln}^{\Phi^{\mathrm{2}} −\varphi\Phi} \left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}},{x}\rightarrow\infty \\ $$$$\Phi^{\mathrm{2}} −\varphi\Phi>\mathrm{0}\:{not}\:{integrable}\:{sir}\:{tcheck}\:{it} \\ $$
Commented by MathSh last updated on 23/Oct/21
$$\mathrm{Yes}\:\mathrm{dear}\:\boldsymbol{\mathrm{Ser}}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
Commented by MathSh last updated on 23/Oct/21

$$\mathrm{Im}\:\mathrm{really}\:\mathrm{sorry}\:\mathrm{dear}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{I}\:\mathrm{had}\:\mathrm{made} \\ $$$$\mathrm{typo}\:\mathrm{this}\:\mathrm{is}\:\mathrm{divergent},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{Ser}} \\ $$
Commented by mindispower last updated on 23/Oct/21
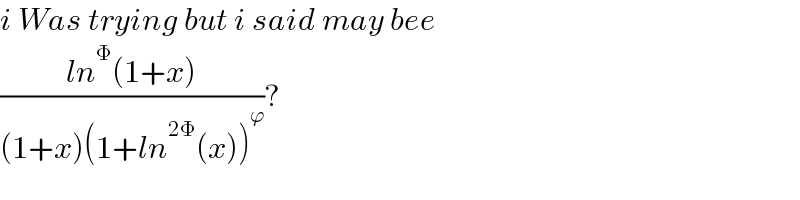
$${i}\:{Was}\:{trying}\:{but}\:{i}\:{said}\:{may}\:{bee} \\ $$$$\frac{{ln}^{\Phi} \left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{ln}^{\mathrm{2}\Phi} \left({x}\right)\right)^{\varphi} }? \\ $$
