Question Number 157455 by aliibrahim1 last updated on 23/Oct/21
Answered by FongXD last updated on 23/Oct/21
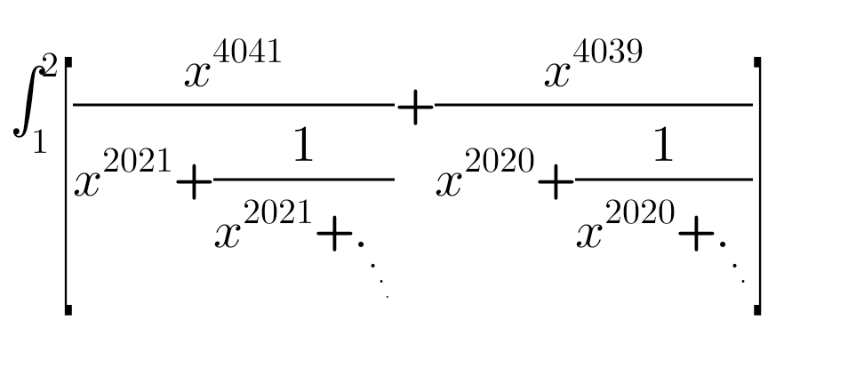
![let u=x^(2021) +(1/(x^(2021) +._._._. ))=x^(2021) +(1/u) ⇔ u^2 −x^(2021) u−1=0, ⇒ u=((x^(2021) +(√(x^(4042) +4)))/2) and v=x^(2020) +(1/(x^(2020) +._._._. ))=x^(2020) +(1/v) ⇔ v^2 −x^(2020) v−1=0, ⇒ v=((x^(2020) +(√(x^(4040) +4)))/2) we get: I=2∫_1 ^2 ((x^(4041) /(x^(2021) +(√(x^(4042) +4))))+(x^(4039) /(x^(2020) +(√(x^(4040) +4)))))dx ⇔ I=−(1/2)∫_1 ^2 [x^(4041) (x^(2021) −(√(x^(4042) +4)))+x^(4039) (x^(2020) −(√(x^(4040) +4)))]dx ⇔ I=−(1/2)∫_1 ^2 (x^(6062) +x^(6059) )dx+(1/2)∫_1 ^2 (1/(4042))(x^(4042) +4)^(1/2) (x^(4042) +4)′dx+(1/2)∫_1 ^2 (1/(4040))(x^(4040) +4)^(1/2) (x^(4040) +4)′dx ⇔ I=−(1/2)[(x^(6063) /(6063))+(x^(6060) /(6060))−((2(x^(4042) +4)^(3/2) )/(3×4042))−((2(x^(4040) +4)^(3/2) )/(3×4040))]_1 ^2 Continue...](https://www.tinkutara.com/question/Q157470.png)
$$\mathrm{let}\:\mathrm{u}=\mathrm{x}^{\mathrm{2021}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2021}} +._{._{._{.} } } }=\mathrm{x}^{\mathrm{2021}} +\frac{\mathrm{1}}{\mathrm{u}} \\ $$$$\Leftrightarrow\:\mathrm{u}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2021}} \mathrm{u}−\mathrm{1}=\mathrm{0},\:\Rightarrow\:\mathrm{u}=\frac{\mathrm{x}^{\mathrm{2021}} +\sqrt{\mathrm{x}^{\mathrm{4042}} +\mathrm{4}}}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{v}=\mathrm{x}^{\mathrm{2020}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2020}} +._{._{._{.} } } }=\mathrm{x}^{\mathrm{2020}} +\frac{\mathrm{1}}{\mathrm{v}} \\ $$$$\Leftrightarrow\:\mathrm{v}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2020}} \mathrm{v}−\mathrm{1}=\mathrm{0},\:\Rightarrow\:\mathrm{v}=\frac{\mathrm{x}^{\mathrm{2020}} +\sqrt{\mathrm{x}^{\mathrm{4040}} +\mathrm{4}}}{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{get}:\:\mathrm{I}=\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{2}} \left(\frac{\mathrm{x}^{\mathrm{4041}} }{\mathrm{x}^{\mathrm{2021}} +\sqrt{\mathrm{x}^{\mathrm{4042}} +\mathrm{4}}}+\frac{\mathrm{x}^{\mathrm{4039}} }{\mathrm{x}^{\mathrm{2020}} +\sqrt{\mathrm{x}^{\mathrm{4040}} +\mathrm{4}}}\right)\mathrm{dx} \\ $$$$\Leftrightarrow\:\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \left[\mathrm{x}^{\mathrm{4041}} \left(\mathrm{x}^{\mathrm{2021}} −\sqrt{\mathrm{x}^{\mathrm{4042}} +\mathrm{4}}\right)+\mathrm{x}^{\mathrm{4039}} \left(\mathrm{x}^{\mathrm{2020}} −\sqrt{\mathrm{x}^{\mathrm{4040}} +\mathrm{4}}\right)\right]\mathrm{dx} \\ $$$$\Leftrightarrow\:\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{6062}} +\mathrm{x}^{\mathrm{6059}} \right)\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{4042}}\left(\mathrm{x}^{\mathrm{4042}} +\mathrm{4}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{x}^{\mathrm{4042}} +\mathrm{4}\right)'\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{4040}}\left(\mathrm{x}^{\mathrm{4040}} +\mathrm{4}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{x}^{\mathrm{4040}} +\mathrm{4}\right)'\mathrm{dx} \\ $$$$\Leftrightarrow\:\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{x}^{\mathrm{6063}} }{\mathrm{6063}}+\frac{\mathrm{x}^{\mathrm{6060}} }{\mathrm{6060}}−\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{4042}} +\mathrm{4}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}×\mathrm{4042}}−\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{4040}} +\mathrm{4}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}×\mathrm{4040}}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\mathrm{Continue}… \\ $$
Commented by aliibrahim1 last updated on 24/Oct/21

$${thx}\:{sir} \\ $$
