Question Number 157538 by ghakhan88 last updated on 24/Oct/21

Commented by ghakhan88 last updated on 24/Oct/21
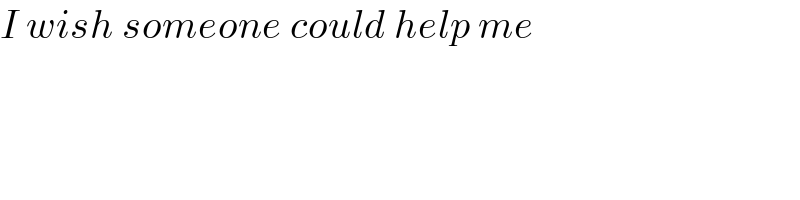
$${I}\:{wish}\:{someone}\:{could}\:{help}\:{me} \\ $$
Answered by metamorfose last updated on 25/Oct/21

$$\left(\bullet\right)\:{u}\left({x}\right)={x}+\mathrm{1}+\int_{\mathrm{0}} ^{{x}} \frac{{t}^{{a}−\mathrm{1}} }{{x}^{{a}} }{u}\left({t}\right){dt} \\ $$$${derivate}\:\left(\bullet\right) \\ $$$${u}'\left({x}\right)=\mathrm{1}+\frac{{u}\left({x}\right)}{{x}}−\frac{{a}}{{x}}\int_{\mathrm{0}} ^{{x}} \frac{{t}^{{a}−\mathrm{1}} }{{x}^{{a}} }{u}\left({t}\right){dt}\:\left(\bullet\bullet\right) \\ $$$$\left(\bullet\right)\:{give}\::\:\int_{\mathrm{0}} ^{{x}} \frac{{t}^{{a}−\mathrm{1}} }{{x}^{{a}} }{u}\left({t}\right){dt}={u}\left({x}\right)−\left({x}+\mathrm{1}\right) \\ $$$${hence}\::\: \\ $$$${u}'\left({x}\right)+\frac{{a}−\mathrm{1}}{{x}}{u}\left({x}\right)=\mathrm{1}−{a}−\frac{{a}}{{x}}\left({ED}\right) \\ $$$$\left({ED}\right)\:{is}\:{a}\:{differential}\:{equation} \\ $$$${type}\:{y}'\left({t}\right)+{a}\left({t}\right){y}\left({t}\right)={b}\left({t}\right)… \\ $$$$ \\ $$
Commented by ghakhan88 last updated on 27/Oct/21

$${I}\:{tried}\:{to}\:{solve}\:{the}\:{eq}\:\left({ED}\right)\:{using}\:{Laplace},\:{and}\:{I}\:{get}\:{rong}\:{answer}! \\ $$
