Question Number 157663 by mathlove last updated on 26/Oct/21

Answered by TheSupreme last updated on 26/Oct/21
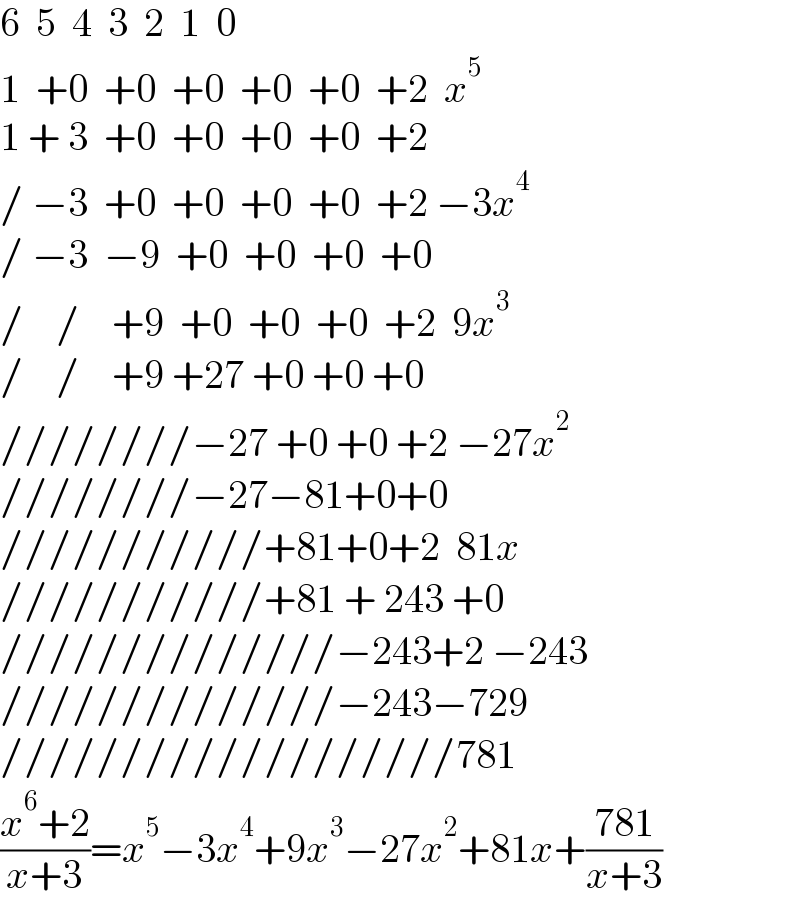
$$\mathrm{6}\:\:\mathrm{5}\:\:\mathrm{4}\:\:\mathrm{3}\:\:\mathrm{2}\:\:\mathrm{1}\:\:\mathrm{0} \\ $$$$\mathrm{1}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{2}\:\:{x}^{\mathrm{5}} \\ $$$$\mathrm{1}\:+\:\mathrm{3}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{2}\:\: \\ $$$$/\:−\mathrm{3}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{2}\:−\mathrm{3}{x}^{\mathrm{4}} \\ $$$$/\:−\mathrm{3}\:\:−\mathrm{9}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0} \\ $$$$/\:\:\:\:/\:\:\:\:+\mathrm{9}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{0}\:\:+\mathrm{2}\:\:\mathrm{9}{x}^{\mathrm{3}} \\ $$$$/\:\:\:\:/\:\:\:\:+\mathrm{9}\:+\mathrm{27}\:+\mathrm{0}\:+\mathrm{0}\:+\mathrm{0}\: \\ $$$$////////−\mathrm{27}\:+\mathrm{0}\:+\mathrm{0}\:+\mathrm{2}\:−\mathrm{27}{x}^{\mathrm{2}} \\ $$$$////////−\mathrm{27}−\mathrm{81}+\mathrm{0}+\mathrm{0} \\ $$$$///////////+\mathrm{81}+\mathrm{0}+\mathrm{2}\:\:\mathrm{81}{x} \\ $$$$///////////+\mathrm{81}\:+\:\mathrm{243}\:+\mathrm{0} \\ $$$$//////////////−\mathrm{243}+\mathrm{2}\:−\mathrm{243} \\ $$$$//////////////−\mathrm{243}−\mathrm{729} \\ $$$$///////////////////\mathrm{781} \\ $$$$\frac{{x}^{\mathrm{6}} +\mathrm{2}}{{x}+\mathrm{3}}={x}^{\mathrm{5}} −\mathrm{3}{x}^{\mathrm{4}} +\mathrm{9}{x}^{\mathrm{3}} −\mathrm{27}{x}^{\mathrm{2}} +\mathrm{81}{x}+\frac{\mathrm{781}}{{x}+\mathrm{3}} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Oct/21
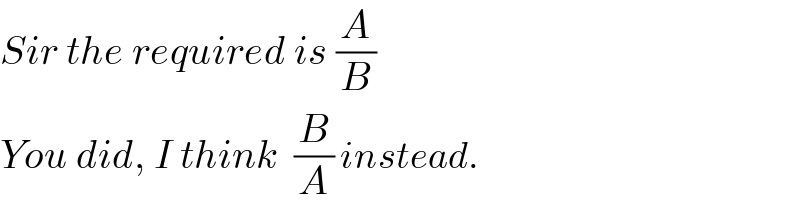
$${Sir}\:{the}\:{required}\:{is}\:\frac{{A}}{{B}} \\ $$$${You}\:{did},\:{I}\:{think}\:\:\frac{{B}}{{A}}\:{instead}. \\ $$
Commented by mathlove last updated on 26/Oct/21

$$\frac{{A}}{{B}}=? \\ $$
Answered by Rasheed.Sindhi last updated on 27/Oct/21
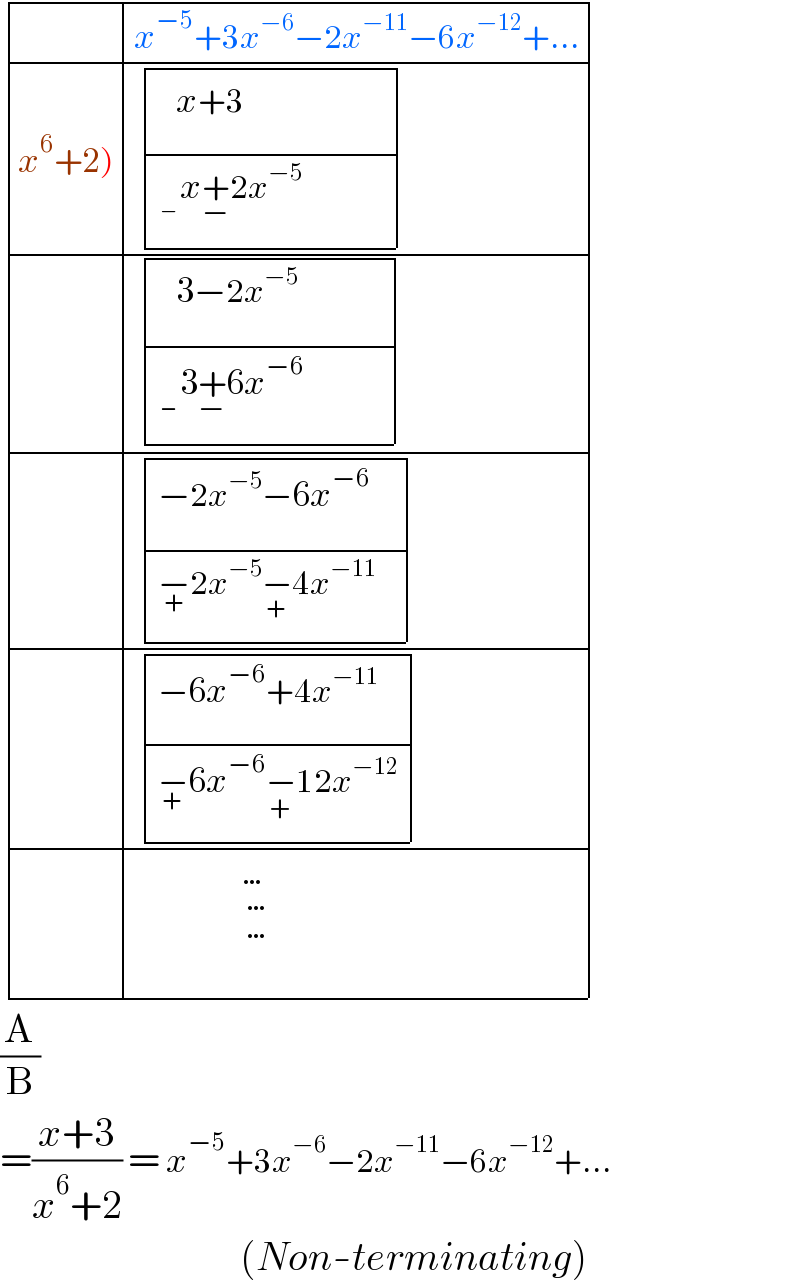
$$\begin{array}{|c|c|c|c|c|c|}{}&\hline{{x}^{−\mathrm{5}} +\mathrm{3}{x}^{−\mathrm{6}} −\mathrm{2}{x}^{−\mathrm{11}} −\mathrm{6}{x}^{−\mathrm{12}} +…}\\{\left.{x}^{\mathrm{6}} +\mathrm{2}\right)}&\hline{\begin{array}{|c|c|}{\:\:\:\underset{} {{x}+\mathrm{3}^{} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}\\{\underset{−} {\:\:\:}{x}\underset{−} {+}\mathrm{2}{x}^{−\mathrm{5}} }\\\hline\end{array}}\\{}&\hline{\begin{array}{|c|c|}{\:\:\:\underset{} {\mathrm{3}−\mathrm{2}{x}^{−\mathrm{5}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:}\\{\underset{−} {\:\:\:}\mathrm{3}\underset{−} {+}\mathrm{6}{x}^{−\mathrm{6}} }\\\hline\end{array}}\\{}&\hline{\begin{array}{|c|c|}{\underset{} {−\mathrm{2}{x}^{−\mathrm{5}} −\mathrm{6}{x}^{−\mathrm{6}} }\:\:\:\:}\\{\underset{+} {−}\mathrm{2}{x}^{−\mathrm{5}} \underset{+} {−}\mathrm{4}{x}^{−\mathrm{11}} }\\\hline\end{array}}\\{}&\hline{\begin{array}{|c|c|}{\underset{} {−\mathrm{6}{x}^{−\mathrm{6}} +\mathrm{4}{x}^{−\mathrm{11}} }}\\{\underset{+} {−}\mathrm{6}{x}^{−\mathrm{6}} \underset{+} {−}\mathrm{12}{x}^{−\mathrm{12}} }\\\hline\end{array}}\\{}&\hline{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{\underset{\:\ldots^{} } {\ldots}} {\ldots}}\\\hline\end{array} \\ $$$$\frac{\mathrm{A}}{\mathrm{B}} \\ $$$$=\frac{{x}+\mathrm{3}}{{x}^{\mathrm{6}} +\mathrm{2}}\:=\:{x}^{−\mathrm{5}} +\mathrm{3}{x}^{−\mathrm{6}} −\mathrm{2}{x}^{−\mathrm{11}} −\mathrm{6}{x}^{−\mathrm{12}} +… \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({Non}-{terminating}\right) \\ $$
Commented by akolade last updated on 28/Oct/21
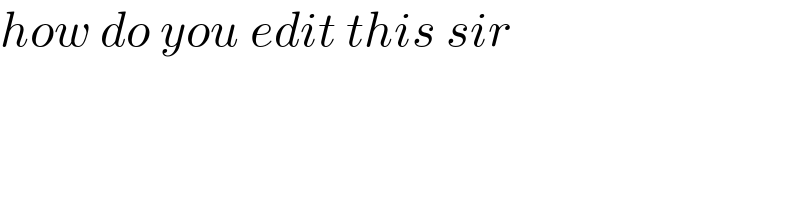
$${how}\:{do}\:{you}\:{edit}\:{this}\:{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 28/Oct/21
![At the bottom of forum-keyboard click ′matrix button′ (seems like this: [(□,□),(□,□) ]),this will open manue of other buttons.click ′table-button′ (seems like this: determinant ((□,□),(□,□))).Click it again when the cursor is in a cell of table.(table within table). You can use ′borderless table button′ also and combine the two. (For me ′borderless-table′ couldn′t be sent).](https://www.tinkutara.com/question/Q157802.png)
$${At}\:{the}\:{bottom}\:{of}\:{forum}-{keyboard} \\ $$$${click}\:'{matrix}\:{button}'\:\left({seems}\:\:{like}\:{this}:\right. \\ $$$$\left.\:\begin{bmatrix}{\Box}&{\Box}\\{\Box}&{\Box}\end{bmatrix}\right),{this}\:{will}\:{open}\:{manue}\:{of} \\ $$$${other}\:{buttons}.{click}\:'{table}-{button}' \\ $$$$\left({seems}\:{like}\:{this}:\begin{array}{|c|c|}{\Box}&\hline{\Box}\\{\Box}&\hline{\Box}\\\hline\end{array}\right).{Click}\:{it} \\ $$$${again}\:{when}\:{the}\:{cursor}\:{is}\:{in}\:{a}\:{cell} \\ $$$$\:{of}\:{table}.\left({table}\:{within}\:{table}\right). \\ $$$${You}\:{can}\:{use}\:'{borderless}\:{table}\:{button}' \\ $$$${also}\:{and}\:{combine}\:{the}\:{two}. \\ $$$$\left({For}\:{me}\:'{borderless}-{table}'\:{couldn}'{t}\right. \\ $$$$\left.{be}\:{sent}\right). \\ $$
