Question Number 157706 by Oberon last updated on 26/Oct/21

Answered by mr W last updated on 26/Oct/21
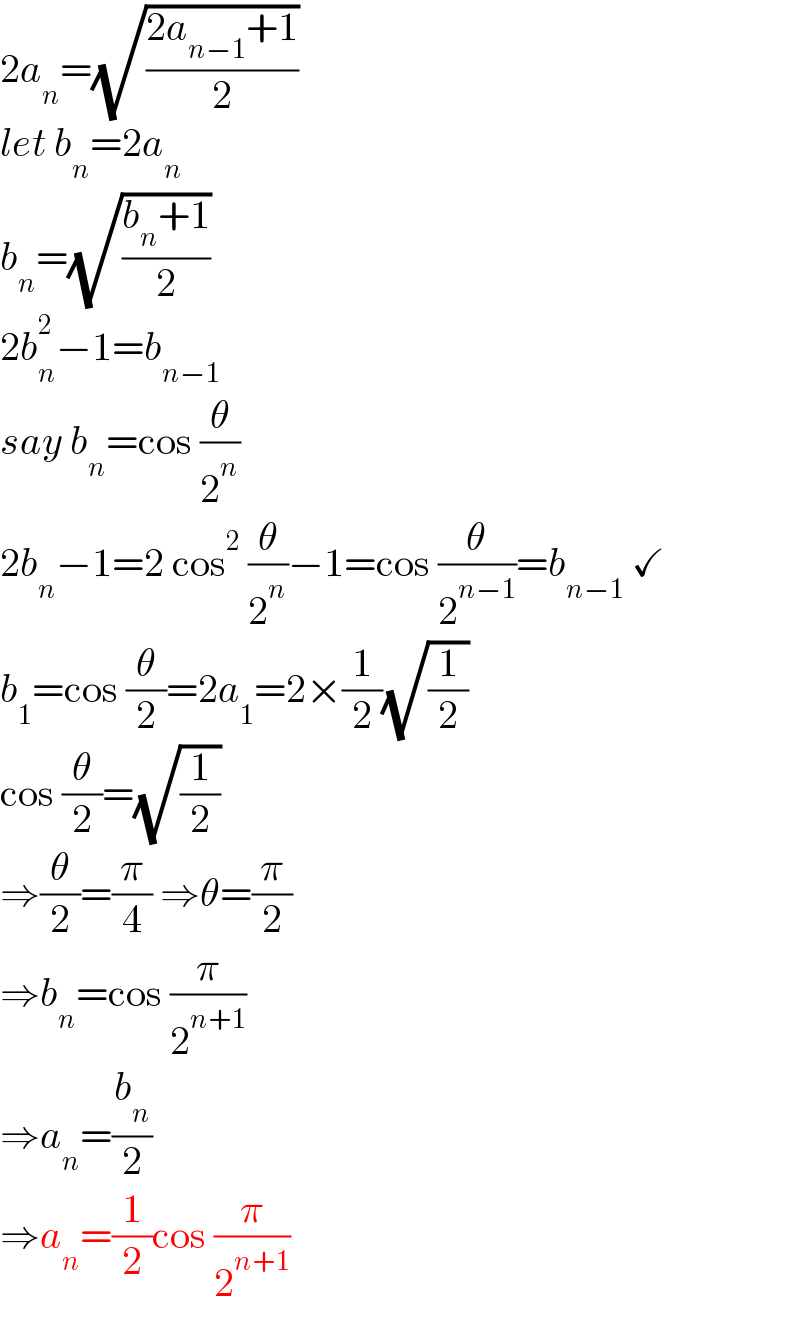
$$\mathrm{2}{a}_{{n}} =\sqrt{\frac{\mathrm{2}{a}_{{n}−\mathrm{1}} +\mathrm{1}}{\mathrm{2}}} \\ $$$${let}\:{b}_{{n}} =\mathrm{2}{a}_{{n}} \\ $$$${b}_{{n}} =\sqrt{\frac{{b}_{{n}} +\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{2}{b}_{{n}} ^{\mathrm{2}} −\mathrm{1}={b}_{{n}−\mathrm{1}} \\ $$$${say}\:{b}_{{n}} =\mathrm{cos}\:\frac{\theta}{\mathrm{2}^{{n}} } \\ $$$$\mathrm{2}{b}_{{n}} −\mathrm{1}=\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}^{{n}} }−\mathrm{1}=\mathrm{cos}\:\frac{\theta}{\mathrm{2}^{{n}−\mathrm{1}} }={b}_{{n}−\mathrm{1}} \:\checkmark \\ $$$${b}_{\mathrm{1}} =\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\mathrm{2}{a}_{\mathrm{1}} =\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow\frac{\theta}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}\:\Rightarrow\theta=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{b}_{{n}} =\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$\Rightarrow{a}_{{n}} =\frac{{b}_{{n}} }{\mathrm{2}} \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$
