Menu Close

Question-157712

Tinku Tara 0 Comments
Pin




Question Number 157712 by ajfour last updated on 26/Oct/21
Commented by ajfour last updated on 26/Oct/21
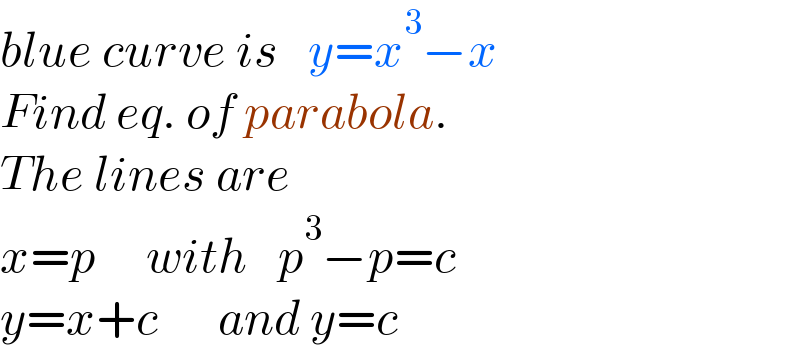
blue curve is y=x^3 −x Find eq. of parabola. The lines are x=p with p^3 −p=c y=x+c and y=c
$${blue}\:{curve}\:{is}\:\:\:{y}={x}^{\mathrm{3}} −{x} \\ $$$${Find}\:{eq}.\:{of}\:{parabola}. \\ $$$${The}\:{lines}\:{are} \\ $$$${x}={p}\:\:\:\:\:{with}\:\:\:{p}^{\mathrm{3}} −{p}={c} \\ $$$${y}={x}+{c}\:\:\:\:\:\:{and}\:{y}={c} \\ $$
Commented by ajfour last updated on 26/Oct/21
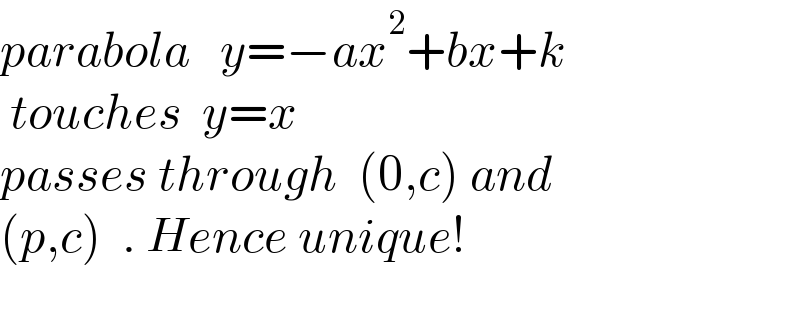
parabola y=−ax^2 +bx+k touches y=x passes through (0,c) and (p,c) . Hence unique!
$${parabola}\:\:\:{y}=−{ax}^{\mathrm{2}} +{bx}+{k} \\ $$$$\:{touches}\:\:{y}={x} \\ $$$${passes}\:{through}\:\:\left(\mathrm{0},{c}\right)\:{and} \\ $$$$\left({p},{c}\right)\:\:.\:{Hence}\:{unique}! \\ $$$$ \\ $$
Answered by ajfour last updated on 26/Oct/21
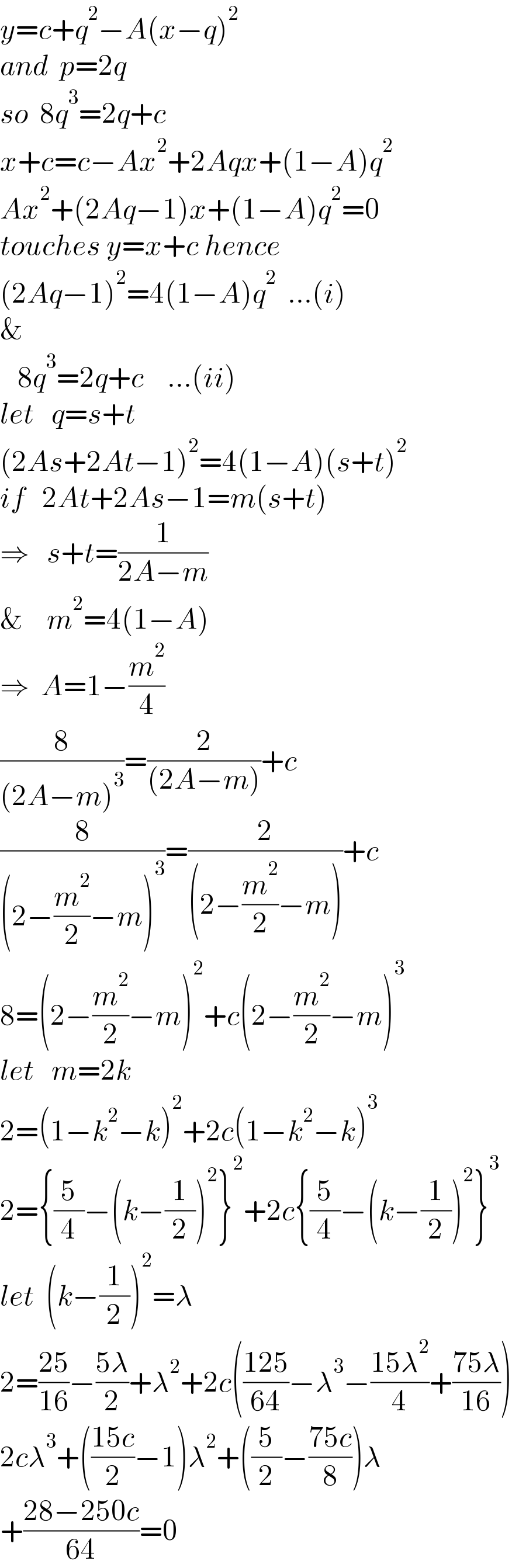
y=c+q^2 −A(x−q)^2 and p=2q so 8q^3 =2q+c x+c=c−Ax^2 +2Aqx+(1−A)q^2 Ax^2 +(2Aq−1)x+(1−A)q^2 =0 touches y=x+c hence (2Aq−1)^2 =4(1−A)q^2 ...(i) & 8q^3 =2q+c ...(ii) let q=s+t (2As+2At−1)^2 =4(1−A)(s+t)^2 if 2At+2As−1=m(s+t) ⇒ s+t=(1/(2A−m)) & m^2 =4(1−A) ⇒ A=1−(m^2 /4) (8/((2A−m)^3 ))=(2/((2A−m)))+c (8/((2−(m^2 /2)−m)^3 ))=(2/((2−(m^2 /2)−m)))+c 8=(2−(m^2 /2)−m)^2 +c(2−(m^2 /2)−m)^3 let m=2k 2=(1−k^2 −k)^2 +2c(1−k^2 −k)^3 2={(5/4)−(k−(1/2))^2 }^2 +2c{(5/4)−(k−(1/2))^2 }^3 let (k−(1/2))^2 =λ 2=((25)/(16))−((5λ)/2)+λ^2 +2c(((125)/(64))−λ^3 −((15λ^2 )/4)+((75λ)/(16))) 2cλ^3 +(((15c)/2)−1)λ^2 +((5/2)−((75c)/8))λ +((28−250c)/(64))=0
$${y}={c}+{q}^{\mathrm{2}} −{A}\left({x}−{q}\right)^{\mathrm{2}} \\ $$$${and}\:\:{p}=\mathrm{2}{q} \\ $$$${so}\:\:\mathrm{8}{q}^{\mathrm{3}} =\mathrm{2}{q}+{c} \\ $$$${x}+{c}={c}−{Ax}^{\mathrm{2}} +\mathrm{2}{Aqx}+\left(\mathrm{1}−{A}\right){q}^{\mathrm{2}} \\ $$$${Ax}^{\mathrm{2}} +\left(\mathrm{2}{Aq}−\mathrm{1}\right){x}+\left(\mathrm{1}−{A}\right){q}^{\mathrm{2}} =\mathrm{0} \\ $$$${touches}\:{y}={x}+{c}\:{hence} \\ $$$$\left(\mathrm{2}{Aq}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−{A}\right){q}^{\mathrm{2}} \:\:…\left({i}\right) \\ $$$$\& \\ $$$$\:\:\:\mathrm{8}{q}^{\mathrm{3}} =\mathrm{2}{q}+{c}\:\:\:\:…\left({ii}\right) \\ $$$${let}\:\:\:{q}={s}+{t} \\ $$$$\left(\mathrm{2}{As}+\mathrm{2}{At}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−{A}\right)\left({s}+{t}\right)^{\mathrm{2}} \\ $$$${if}\:\:\:\mathrm{2}{At}+\mathrm{2}{As}−\mathrm{1}={m}\left({s}+{t}\right) \\ $$$$\Rightarrow\:\:\:{s}+{t}=\frac{\mathrm{1}}{\mathrm{2}{A}−{m}} \\ $$$$\&\:\:\:\:{m}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−{A}\right) \\ $$$$\Rightarrow\:\:{A}=\mathrm{1}−\frac{{m}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\frac{\mathrm{8}}{\left(\mathrm{2}{A}−{m}\right)^{\mathrm{3}} }=\frac{\mathrm{2}}{\left(\mathrm{2}{A}−{m}\right)}+{c} \\ $$$$\frac{\mathrm{8}}{\left(\mathrm{2}−\frac{{m}^{\mathrm{2}} }{\mathrm{2}}−{m}\right)^{\mathrm{3}} }=\frac{\mathrm{2}}{\left(\mathrm{2}−\frac{{m}^{\mathrm{2}} }{\mathrm{2}}−{m}\right)}+{c} \\ $$$$\mathrm{8}=\left(\mathrm{2}−\frac{{m}^{\mathrm{2}} }{\mathrm{2}}−{m}\right)^{\mathrm{2}} +{c}\left(\mathrm{2}−\frac{{m}^{\mathrm{2}} }{\mathrm{2}}−{m}\right)^{\mathrm{3}} \\ $$$${let}\:\:\:{m}=\mathrm{2}{k} \\ $$$$\mathrm{2}=\left(\mathrm{1}−{k}^{\mathrm{2}} −{k}\right)^{\mathrm{2}} +\mathrm{2}{c}\left(\mathrm{1}−{k}^{\mathrm{2}} −{k}\right)^{\mathrm{3}} \\ $$$$\mathrm{2}=\left\{\frac{\mathrm{5}}{\mathrm{4}}−\left({k}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} +\mathrm{2}{c}\left\{\frac{\mathrm{5}}{\mathrm{4}}−\left({k}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right\}^{\mathrm{3}} \\ $$$${let}\:\:\left({k}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\lambda \\ $$$$\mathrm{2}=\frac{\mathrm{25}}{\mathrm{16}}−\frac{\mathrm{5}\lambda}{\mathrm{2}}+\lambda^{\mathrm{2}} +\mathrm{2}{c}\left(\frac{\mathrm{125}}{\mathrm{64}}−\lambda^{\mathrm{3}} −\frac{\mathrm{15}\lambda^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{75}\lambda}{\mathrm{16}}\right) \\ $$$$\mathrm{2}{c}\lambda^{\mathrm{3}} +\left(\frac{\mathrm{15}{c}}{\mathrm{2}}−\mathrm{1}\right)\lambda^{\mathrm{2}} +\left(\frac{\mathrm{5}}{\mathrm{2}}−\frac{\mathrm{75}{c}}{\mathrm{8}}\right)\lambda \\ $$$$+\frac{\mathrm{28}−\mathrm{250}{c}}{\mathrm{64}}=\mathrm{0} \\ $$
Answered by mr W last updated on 27/Oct/21
Commented by mr W last updated on 27/Oct/21
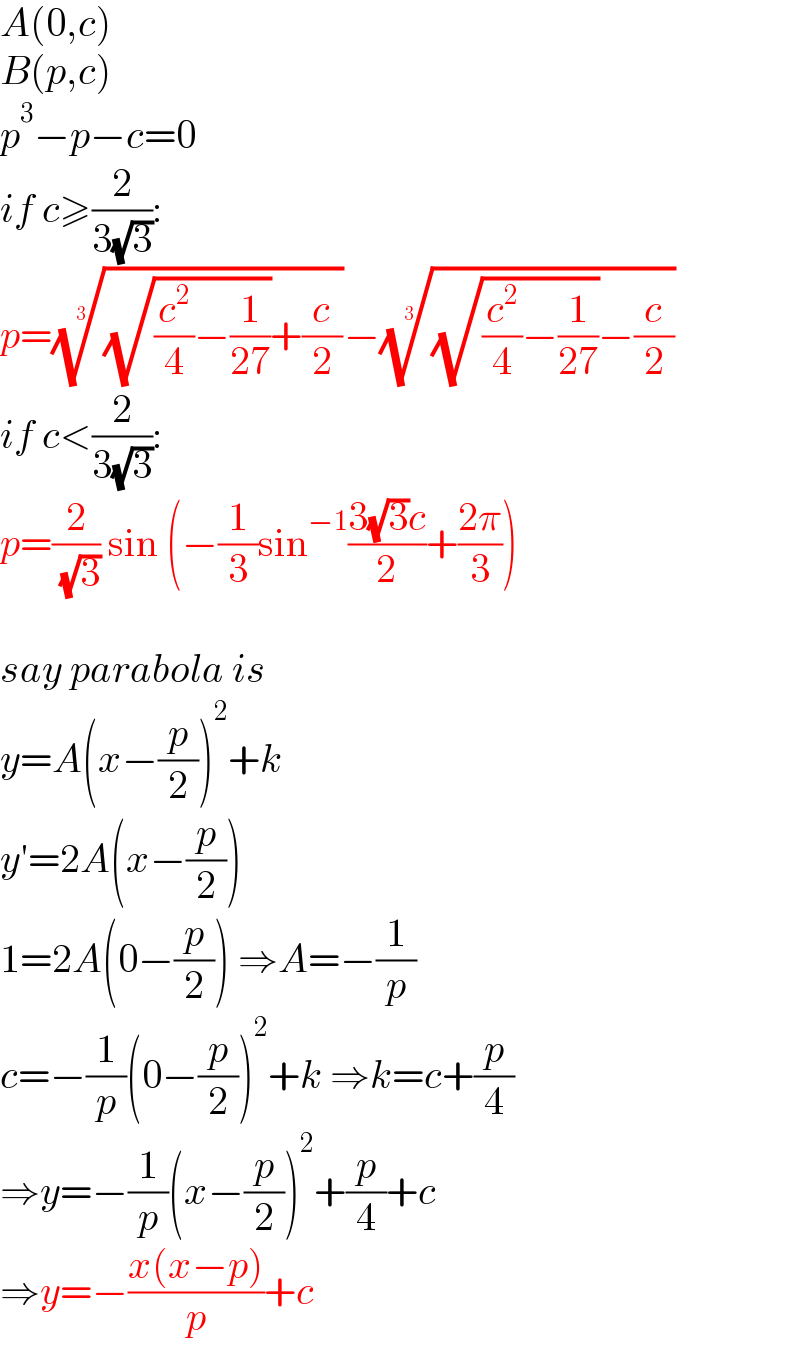
A(0,c) B(p,c) p^3 −p−c=0 if c≥(2/(3(√3))): p=(((√((c^2 /4)−(1/(27))))+(c/2)))^(1/3) −(((√((c^2 /4)−(1/(27))))−(c/2)))^(1/3) if c<(2/(3(√3))): p=(2/( (√3))) sin (−(1/3)sin^(−1) ((3(√3)c)/2)+((2π)/3)) say parabola is y=A(x−(p/2))^2 +k y′=2A(x−(p/2)) 1=2A(0−(p/2)) ⇒A=−(1/p) c=−(1/p)(0−(p/2))^2 +k ⇒k=c+(p/4) ⇒y=−(1/p)(x−(p/2))^2 +(p/4)+c ⇒y=−((x(x−p))/p)+c
$${A}\left(\mathrm{0},{c}\right) \\ $$$${B}\left({p},{c}\right) \\ $$$${p}^{\mathrm{3}} −{p}−{c}=\mathrm{0} \\ $$$${if}\:{c}\geqslant\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}: \\ $$$${p}=\sqrt[{\mathrm{3}}]{\sqrt{\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{27}}}+\frac{{c}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{27}}}−\frac{{c}}{\mathrm{2}}} \\ $$$${if}\:{c}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}: \\ $$$${p}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{sin}\:\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}\sqrt{\mathrm{3}}{c}}{\mathrm{2}}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$ \\ $$$${say}\:{parabola}\:{is} \\ $$$${y}={A}\left({x}−\frac{{p}}{\mathrm{2}}\right)^{\mathrm{2}} +{k} \\ $$$${y}'=\mathrm{2}{A}\left({x}−\frac{{p}}{\mathrm{2}}\right) \\ $$$$\mathrm{1}=\mathrm{2}{A}\left(\mathrm{0}−\frac{{p}}{\mathrm{2}}\right)\:\Rightarrow{A}=−\frac{\mathrm{1}}{{p}} \\ $$$${c}=−\frac{\mathrm{1}}{{p}}\left(\mathrm{0}−\frac{{p}}{\mathrm{2}}\right)^{\mathrm{2}} +{k}\:\Rightarrow{k}={c}+\frac{{p}}{\mathrm{4}} \\ $$$$\Rightarrow{y}=−\frac{\mathrm{1}}{{p}}\left({x}−\frac{{p}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{p}}{\mathrm{4}}+{c} \\ $$$$\Rightarrow{y}=−\frac{{x}\left({x}−{p}\right)}{{p}}+{c} \\ $$
Commented by mr W last updated on 27/Oct/21
Commented by mr W last updated on 27/Oct/21
Commented by ajfour last updated on 27/Oct/21
thank you sir!
$${thank}\:{you}\:{sir}!\: \\ $$
Commented by Ahmed1hamouda last updated on 29/Oct/21
What applications do you use in thee enginering solution
$$\mathrm{What}\:\mathrm{applications}\:\mathrm{do}\:\mathrm{you}\:\mathrm{use}\:\mathrm{in}\:\mathrm{thee} \\ $$$$\mathrm{enginering}\:\mathrm{solution} \\ $$
Commented by mr W last updated on 29/Oct/21
Grapher
$${Grapher} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *